题目内容
若(1-2x)2014=a0+a1x+a2x2+…+a2014x2014(x∈R),则
+
+
+…+
的值为( )
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
| A、-1 | B、0 | C、2 | D、-2 |
考点:二项式系数的性质
专题:二项式定理
分析:由题意可得a0=1,令x=
,可得0=1+
+
+
+…+
,由此求得所求式子的值.
| 1 |
| 2 |
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
解答:
解:在 (1-2x)2014=a0+a1x+a2x2+…+a2014x2014(x∈R)中,易知a0=1,
令x=
,可得0=1+
+
+
+…+
,
∴
+
+
+…+
=-1,
故选:A.
令x=
| 1 |
| 2 |
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
∴
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
故选:A.
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在四面体ABCD中,已知AB=x,该四面体的其余五条棱的长度均为2,则下列说法中错误的是( )
A、棱长x的取值范围是:0<x<2
| ||
| B、该四面体一定满足:AB⊥CD | ||
C、当x=2
| ||
| D、当x=2时,该四面体的体积最大 |
下列关于两条不同的直线l,m两个不重合的平面α,β的说法,正确的是( )
| A、若l?α且α⊥β,则l⊥β |
| B、若l⊥β且m⊥β,则l∥m |
| C、若l⊥β且α⊥β,则l∥α |
| D、若α∩β=m且l⊥m,则l⊥α |
i是虚数单位,i(-1+2i)=( )
| A、i+2 | B、i-2 |
| C、-2-i | D、2-i |
已知全集U={x∈Z|1≤x≤5},A={1,2,3},∁UB={1,2},则A∩B( )
| A、{1,2} |
| B、{1,3} |
| C、{3} |
| D、{1,2,3} |
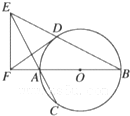 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.