题目内容
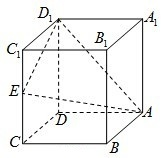 如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )
如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )| A、圆 | B、椭圆 | C、抛物线 | D、线段 |
考点:抛物线的定义
专题:计算题,空间位置关系与距离
分析:取棱BB1的中点N,棱B1C1的中点,证明平面A1NM∥平面AED1,F是侧面B1BCC1上的动点,可得F是线段MN上的点时,A1F∥平面AED1,即可得出结论.
解答:
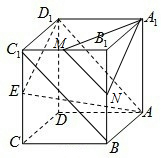 解:取棱BB1的中点N,棱B1C1的中点,则MN∥BC1,
解:取棱BB1的中点N,棱B1C1的中点,则MN∥BC1,
∵BC1∥AD1,
∴MN∥AD1,
∵MN?平面AED1,AD1?平面AED1,
∴MN∥平面AED1,
同理,A1N∥平面AED1,
∵MN∩A1N=N,
∴平面A1NM∥平面AED1,
∵F是侧面B1BCC1上的动点,
∴F是线段MN上的点时,A1F∥平面AED1,
故选:D.
 解:取棱BB1的中点N,棱B1C1的中点,则MN∥BC1,
解:取棱BB1的中点N,棱B1C1的中点,则MN∥BC1,∵BC1∥AD1,
∴MN∥AD1,
∵MN?平面AED1,AD1?平面AED1,
∴MN∥平面AED1,
同理,A1N∥平面AED1,
∵MN∩A1N=N,
∴平面A1NM∥平面AED1,
∵F是侧面B1BCC1上的动点,
∴F是线段MN上的点时,A1F∥平面AED1,
故选:D.
点评:本题考查轨迹问题,考查线面平行,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
对具有线性相关关系的变量x,y,测得一组数据如下表:
参考公式:b=
根据上表,利用最小二乘法得它们的回归直线方程为
=bx+1.5,据此模型来预测当x=20时,y的估计值为( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
| |||||||
|
| ∧ |
| y |
| A、210.5 | B、212.5 |
| C、210 | D、211.5 |
设
,
是两个非零向量,则使
•
=|
||
|成立的一个必要非充分条件是( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
i是虚数单位,i(-1+2i)=( )
| A、i+2 | B、i-2 |
| C、-2-i | D、2-i |

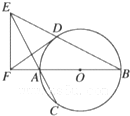 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.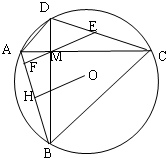 如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,求证:
如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,求证: