题目内容
给出如下四个命题:
①若“p且q”为假命题,则p、q均为假命题;
②命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;
③命题“对任意的x∈R,x2+1≥1”的否定是“存在x∈R,x2+1<1”;
④在△ABC中,“A>B”是“cosA<cosB”的充要条件,其中不正确的命题的个数是( )
①若“p且q”为假命题,则p、q均为假命题;
②命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;
③命题“对任意的x∈R,x2+1≥1”的否定是“存在x∈R,x2+1<1”;
④在△ABC中,“A>B”是“cosA<cosB”的充要条件,其中不正确的命题的个数是( )
| A、4 | B、3 | C、2 | D、1 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用“且命题”的意义即可判断出;
②利用命题的否命题定义即可得出;
③利用全称命题的否定是特称命题即可得出;
④在△ABC中,0<A<B<π,由余弦函数在(0,π)上单调递减,即可判断出.
②利用命题的否命题定义即可得出;
③利用全称命题的否定是特称命题即可得出;
④在△ABC中,0<A<B<π,由余弦函数在(0,π)上单调递减,即可判断出.
解答:
解:①若“p且q”为假命题,则p、q至少有一个为假命题,因此①不正确;
②命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”,正确;
③命题“对任意的x∈R,x2+1≥1”的否定是“存在x∈R,x2+1<1”,正确;
④在△ABC中,0<A<B<π,由余弦函数在(0,π)上单调递减,∴“cosA<cosB”?A<B.
∴在△ABC中,“A>B”是“cosA<cosB”的充要条件,正确.
综上可知:不正确的命题的个数是1.
故选:D.
②命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”,正确;
③命题“对任意的x∈R,x2+1≥1”的否定是“存在x∈R,x2+1<1”,正确;
④在△ABC中,0<A<B<π,由余弦函数在(0,π)上单调递减,∴“cosA<cosB”?A<B.
∴在△ABC中,“A>B”是“cosA<cosB”的充要条件,正确.
综上可知:不正确的命题的个数是1.
故选:D.
点评:本题考查了简易逻辑的有关知识、三角函数的和差化积及其正弦函数的单调性,属于基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
i是虚数单位,i(-1+2i)=( )
| A、i+2 | B、i-2 |
| C、-2-i | D、2-i |
已知全集U={x∈Z|1≤x≤5},A={1,2,3},∁UB={1,2},则A∩B( )
| A、{1,2} |
| B、{1,3} |
| C、{3} |
| D、{1,2,3} |
 如图,在△ABC中,已知AB=10,AC=14,B=
如图,在△ABC中,已知AB=10,AC=14,B=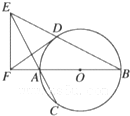 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.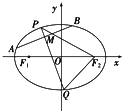 已知椭圆C:
已知椭圆C: