题目内容
设复数z=
，则复数z2的实部与虚部的和为（ ）
| 2i |
| -1+i |
| A、0 | B、2 | C、-2 | D、4 |
考点：复数的基本概念
专题：数系的扩充和复数
分析：由复数的除法运算化简，求得实部和虚部后求和得答案．
解答：
解：∵z=
=
=
=1-i．
∴z2=（1-i）2=-2i．
∴复数z2的实部与虚部的和为-2
故选：C．
| 2i |
| -1+i |
| 2i(-1-i) |
| (-1+i)(-1-i) |
| 2-2i |
| 2 |
∴z2=（1-i）2=-2i．
∴复数z2的实部与虚部的和为-2
故选：C．
点评：本题考查了复数的除法运算，考查了复数的基本概念，是基础的计算题．
练习册系列答案
出彩同步大试卷系列答案
相关题目
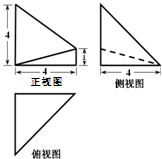已知某几何体的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形，则此几何体的体积V为（ ）A、
| ||
B、
| ||
C、
| ||
| D、40 |
已知函数f（x）为奇函数，且当x＜0时，f（x）=x2+2x，则f（1）=（ ）
| A、1 | B、-1 | C、3 | D、-3 |
对具有线性相关关系的变量x，y，测得一组数据如下表：
参考公式：b=
根据上表，利用最小二乘法得它们的回归直线方程为
=bx+1.5，据此模型来预测当x=20时，y的估计值为（ ）
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
| |||||||
|
| ∧ |
| y |
| A、210.5 | B、212.5 |
| C、210 | D、211.5 |
在四面体ABCD中，已知AB=x，该四面体的其余五条棱的长度均为2，则下列说法中错误的是（ ）
A、棱长x的取值范围是：0＜x＜2
| ||
| B、该四面体一定满足：AB⊥CD | ||
C、当x=2
| ||
| D、当x=2时，该四面体的体积最大 |
如图，在△ABC中，已知AB=10，AC=14，B=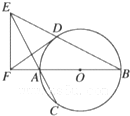
如图，AB是⊙O的直径，弦BD、CA的延长线相交于点E，EF垂直BA的延长线于点F．求证．