题目内容
已知正四棱锥P-ABCD的棱长为2
a,侧面等腰三角形的顶角为30°,则从点A出发,环绕侧面一周后回到A点的最短路程等于 .
| 3 |
考点:多面体和旋转体表面上的最短距离问题
专题:计算题,空间位置关系与距离
分析:用空间思维将此正四棱锥的侧面展开,得到一个由四个全等的顶角为30°的等腰三角形组成的图形,所求的路径,是一个以2
a为腰长,120°为顶角的三角形的底边,由余弦定理可得最短路程.
| 3 |
解答:
解:用空间思维将此正四棱锥的侧面展开,得到一个由四个全等的顶角为30°的等腰三角形组成的图形,
所求的路径,是一个以2
a为腰长,120°为顶角的三角形的底边,
由余弦定理可得最短路程等于
=6a.
故答案为:6a.
所求的路径,是一个以2
| 3 |
由余弦定理可得最短路程等于
12a2+12a2-2•2
|
故答案为:6a.
点评:本题考查正四棱锥的侧面展开图,考查余弦定理,考查学生的计算能力,正确运用正四棱锥的侧面展开图是关键.

练习册系列答案
相关题目
一个棱锥的三视图如图所示,则这个棱锥的体积为( )


| A、12 | B、36 | C、16 | D、48 |
设
,
是非零向量,则“
-
=
”是“
∥
”的( )
| a |
| b |
| a |
| b |
| 0 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
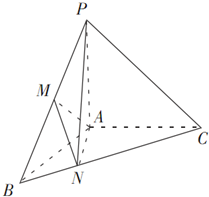 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN. 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若PA=AB=BC=