题目内容
已知圆C:(x-2)2+y2=1,点P在直线l:x+y+1=0上,若过点P存在直线m与圆C交于A、B两点,且点A为PB的中点,则点P横坐标x0的取值范围是 .
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:设点P(x0,-x0-1),B(2+cosθ,sinθ),求出A的坐标,代入圆C:(x-2)2+y2=1,利用辅助角公式,即可确定点P横坐标x0的取值范围.
解答:
解:设点P(x0,-x0-1),B(2+cosθ,sinθ),则
由条件得A点坐标为x=
,y=
,
从而(
-2)2+(
)2=1,
整理得x02+(cosθ-sinθ-1)x0+1-2cosθ-sinθ=0,
化归为(x0-2)cosθ-(x0+1)sinθ+x02-x0+1=0,
从而
sin(θ+ϕ)=-x02+x0-1,
于是由(
)2≥(-x02+x0-1)2,解得-1≤x0≤2.
故答案为:[-1,2].
由条件得A点坐标为x=
| x0+2+cosθ |
| 2 |
| sinθ-x0-1 |
| 2 |
从而(
| x0+2+cosθ |
| 2 |
| sinθ-x0-1 |
| 2 |
整理得x02+(cosθ-sinθ-1)x0+1-2cosθ-sinθ=0,
化归为(x0-2)cosθ-(x0+1)sinθ+x02-x0+1=0,
从而
| 2x02-2x0+5 |
于是由(
| 2x02-2x0+5 |
故答案为:[-1,2].
点评:本题考查直线与圆的位置关系,考查参数法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
已知点P(x,y)满足线性约束条件
,点M(3,1),O为坐标原点,则
•
的最大值为( )
|
| OM |
| OP |
| A、12 | B、11 | C、3 | D、-1 |
已知等差数列{an}中,a7=
,则a6+a7+a8等于( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、111 |
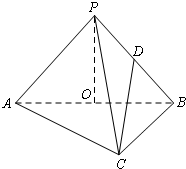 如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,连结CD.
如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,连结CD.