题目内容
已知数列{an}满足a1=100，an+1-an=2n，则
的最小值 ．
| an |
| n |
考点：数列递推式
专题：综合题,等差数列与等比数列
分析：a2-a1=2，a3-a2=4，…，an+1-an=2n，这n个式子相加，就有an+1=100+n（n+1），故an=n（n-1）+100=n2-n+100，可得
=n+
-1，利用基本不等式，即可求出
的最小值．
| an |
| n |
| 100 |
| n |
| an |
| n |
解答：
解：a2-a1=2，
a3-a2=4，
…
an+1-an=2n，
这n个式子相加，就有an+1=100+n（n+1），
即an=n（n-1）+100=n2-n+100，
∴
=n+
-1≥2
-1=19，
当且仅当n=
，即n=10时，
取最小值19．
故答案为：19．
a3-a2=4，
…
an+1-an=2n，
这n个式子相加，就有an+1=100+n（n+1），
即an=n（n-1）+100=n2-n+100，
∴
| an |
| n |
| 100 |
| n |
n•
|
当且仅当n=
| 100 |
| n |
| an |
| n |
故答案为：19．
点评：本题考查数列的性质和应用，考查叠加法，考查基本不等式的运用，确定
=n+
-1是关键．
| an |
| n |
| 100 |
| n |
练习册系列答案
相关题目
执行如图的程序框图，则输出的S值等于（ ）
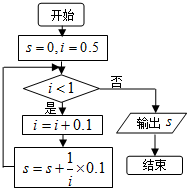
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
已知正三棱柱ABC-A1B1C的底面边长为4cm，高为7cm，则当一质点自点A出发，沿着三棱柱的侧面绕行两周到达点A1的路程最短时，质点沿着侧面的前进方向所在直线与底面ABC所成角的余弦值为已知向量
=（-3，2），
=（2，m）且
⊥
，则m=（ ）
| a |
| b |
| a |
| b |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
经调查发现，人们长期食用含高浓度甲基汞的鱼类会引起汞中毒，其中罗非鱼体内汞含量比其它鱼偏高．现从一批数量很大的罗非鱼中随机地抽出15条作样本，经检测得各条鱼的汞含量的茎叶图（以小数点前的数字为茎，小数点后一位数字为叶）如图．《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm．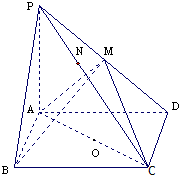
在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M，交PC于点N．