题目内容
已知函数f(x)=
sinxcosx-cos2x+
.
(Ⅰ)求f(x)的最小正周期及对称轴方程;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,若f(
)=
,bc=6,求a的最小值.
| 3 |
| 1 |
| 2 |
(Ⅰ)求f(x)的最小正周期及对称轴方程;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,若f(
| A |
| 2 |
| 1 |
| 2 |
考点:余弦定理,三角函数中的恒等变换应用
专题:三角函数的求值
分析:(Ⅰ)f(x)解析式利用二倍角的正弦、余弦函数公式化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,找出ω的值,代入周期公式即可求出f(x)的最小正周期,根据正弦函数的对称性即可确定出对称轴方程;
(Ⅱ)由f(
)=
,根据第一问确定出的f(x)解析式,求出A的度数,利用余弦定理列出关系式,利用完全平方公式变形后,将cosA,bc的值代入,利用基本不等式求出a的最小值即可.
(Ⅱ)由f(
| A |
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)f(x)=
sin2x-
cos2x=sin(2x-
),
∵ω=2,
∴f(x)的最小正周期T=
=π,
令2x-
=kπ+
,得到x=
+
(k∈Z),
则图象的对称轴方程为x=
+
(k∈Z);
(Ⅱ)由f(
)=sin(A-
)=
,得到A-
=
或A-
=
,
解得:A=
或A=π(舍去),
∵bc=6,
∴由余弦定理得:a2=b2+c2-2bccosA=b2+c2-bc≥bc=6,
当且仅当b=c时等号成立,
则a的最小值为
.
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∵ω=2,
∴f(x)的最小正周期T=
| 2π |
| 2 |
令2x-
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 3 |
则图象的对称轴方程为x=
| kπ |
| 2 |
| π |
| 3 |
(Ⅱ)由f(
| A |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
解得:A=
| π |
| 3 |
∵bc=6,
∴由余弦定理得:a2=b2+c2-2bccosA=b2+c2-bc≥bc=6,
当且仅当b=c时等号成立,
则a的最小值为
| 6 |
点评:此题考查了余弦定理,平面向量的数量积运算,正弦函数的对称性,以及基本不等式的运用,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
下列命题中正确的是( )
| A、20.3>1>0.32 | ||||
| B、?m,n∈R+,lg(m+n)=lgm•lgn | ||||
C、0.31
| ||||
D、如果a
|
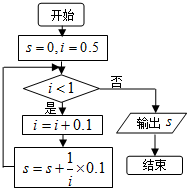
执行如图的程序框图,则输出的S值等于( )

A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
 如图,焦距为2的椭圆E的两个顶点分别为A和B,且
如图,焦距为2的椭圆E的两个顶点分别为A和B,且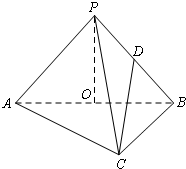 如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,连结CD.
如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,连结CD. 经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如图.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm.
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如图.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm.