题目内容

一个棱锥的三视图如图所示，则这个棱锥的体积为（　　）
A、12B、36C、16D、48
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体是四棱锥，再根据三视图判断四棱锥的高与底面长方形的长与宽，把数据代入棱锥的体积计算可得答案．
解答： 解：由三视图知几何体是四棱锥，且四棱锥的一条侧棱与底面垂直，高为3，
四棱锥的底面是长方形，长方形的长、宽分别为4、3，
∴几何体的体积V=
1
3
×3×4×3=12．
故选：A．
点评：本题考查了由三视图求几何体的体积，解题的关键是判断几何体的形状及数据所对应的几何量．
练习册系列答案
相关题目
函数f（x）=2sin（πx）-
1
1-x
，x∈[-2，4]的所有零点之和为
 
．
下列命题中正确的是（　　）
A、20.3＞1＞0.32
B、?m，n∈R+，lg（m+n）=lgm•lgn
C、0.31
6
5
＞0.35
6
5
D、如果a
1
2
=b，则logab=
1
2
如图程序输出的结果是（　　）
A、3B、7C、15D、19
执行如图的程序框图．若输入n=7，则输出的值为（　　）
A、2B、3C、4D、5
已知点P（x，y）满足线性约束条件
y≤2
x+y≥1
x-y≤1
，点M（3，1），O为坐标原点，则
OM
•
OP
的最大值为（　　）
A、12B、11C、3D、-1
执行如图的程序框图，则输出的S值等于（　　）
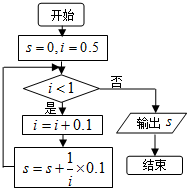
A、
1
6
+
1
7
+
1
8
+
1
9
B、
1
5
+
1
6
+
1
7
+
1
8
+
1
9
C、
1
6
+
1
7
+
1
8
+
1
9
+
1
10
D、
1
5
+
1
6
+
1
7
+
1
8
+
1
9
+
1
10
设数列{an}的前n项和为Sn，已知a1=2，3Sn=an+1+(-2)n+2-6，n∈N*．
（1）求a2的值；
（2）求数列{an}的通项公式；
（3）证明：对一切正整数n，有
1
a1
+
1
a2
+…+
1
an
＜
7
12
．
已知正四棱锥P-ABCD的棱长为2
3
a，侧面等腰三角形的顶角为30°，则从点A出发，环绕侧面一周后回到A点的最短路程等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网