题目内容
已知数列{an}的前n项和,Sn=n2+2n.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)记Tn=
+
+…+
,求Tn.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)记Tn=
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:(I)当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1即可得出.
(II)利用“裂项求和”即可得出.
(II)利用“裂项求和”即可得出.
解答:
解:(I)当n=1时,a1=S1=3,
当n≥2时,an=Sn-Sn-1=2n+1,
又n=1适合上式,
∴an=2n+1,n∈N*.
(II)∵
=
=
(
-
),
∴Tn=
[(
-
)+(
-
)+…+(
-
)]
=
(
-
)
=
-
.
当n≥2时,an=Sn-Sn-1=2n+1,
又n=1适合上式,
∴an=2n+1,n∈N*.
(II)∵
| 1 |
| anan+1 |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n+3 |
=
| 1 |
| 6 |
| 1 |
| 4n+6 |
点评:本题考查了利用“当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1”求数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
已知θ∈R时,不等式m2-(1+4sin2θ)m+4-6cos2θ≥0恒成立,则实数m的取值范围是( )
| A、m≥4或m≤1 |
| B、m≥4或m≤-1 |
| C、m≥2或m≤1 |
| D、m≥2或m≤-1 |
某种商品若每个售价60元,则可卖出50个;已知单价每提高10元,则少卖5个,要得到最大的售货金额,售价应定为( )
| A、80元 | B、85元 |
| C、90元 | D、100元 |
在△ABC中,
=(cos23°,sin23°),
=(2sin22°,2cos22°),则△ABC的面积为( )
| AB |
| AC |
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
已知全集为U,集合A、B均为U的子集,则A∩∁UB=∅是A∪B=B的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
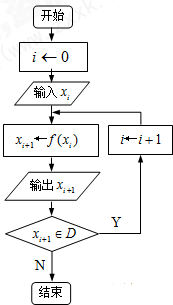 对任意函数f(x),x∈D,可按如图构造一个数列发生器,由数列发生器产生的数列记为{xn}.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,由数列发生器产生的数列记为{xn}.