题目内容

若圆x2+y2+2x-2（a+1）y+3a2+3a+1=0上的所有点都在第二象限，则实数a的取值范围为
 
．
考点：圆的一般方程
专题：直线与圆
分析：把圆的方程化为标准方程后找出圆心坐标和半径，根据第二象限的点横坐标小于0，纵坐标大于0，且横、纵坐标的绝对值大于半径，得到关于a的不等式，求出a的范围即可．
解答： 解：把圆的方程化为标准形式得（x+1）2+[y-（a+1）]2 =-2a2-a+1，所以圆心（-1，a+1），半径等于
-2a2-a+1
，
由圆上的所有点都在第二象限，可得
-2a2-a+1＞0
-2a2-a+1＜1
-2a2-a+1＜|a+1|2
a+1＞0
，求得0＜a＜
1
2
，
故答案为：（0，
1
2
）．
点评：本题主要考查圆的一般方程和圆的标准方程，掌握第二象限点横坐标小于0纵坐标大于0的特点，是一道基础题．
练习册系列答案
相关题目
求函数y=x（4-x）（O＜x＜4）的最大值，并求取大值时的x的值．
已知数列{an}满足：an+1=
an(an2+3)
3an2+1
，a1=2，bn=
an-1
an+1

（1）求{bn}的通项公式；
（2）求证：当n≥3时，b1+b2+…+bn＜
241
648
．
（理）若函数f（x）在给定区间M上存在正数t，使得对任意x∈M，有x+t∈M，且f（x+t）≥f（x），则称f（x）为M上的t级类增函数．给出下列命题：
①函数f（x）=3x是 R上的1级类增函数；
②若函数f（x）=sinx+ax为[
π
2
，+∞）上的
π
3
级类增函数，则实数a的最小值为2；
③若函数f（x）=x2-3x为[1，+∞）上的t级类增函数，则实数t的取值范围为[1，+∞）．
其中正确命题的个数为（　　）
A、0B、1C、2D、3
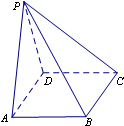如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，且PA=PD=
2
2
AD．
（1）求证：CD⊥平面PAD；
（2）求证：平面PAB⊥平面PCD；
（3）除了已知和（2）中的两个平面互相垂直以外，在不添加其它点和线的情况下，图中还有哪些平面是互相垂直的？
若二项式(x3+
1
2
x
)n的展开式中含有非零常数项，则正整数n的最小值为
 
．
已知f（x）=
m
x+1
+nlnx（m，n为常数），在x=1处的切线为x+y-2=0．
（1）求y=f（x）的单调区间；
（2）若任意实数x∈[
1
e
，1]，使得对任意的t∈[1，2]上恒有f（x）≥t3-t2-2at成立，求实数a的取值范围．
已知直线l1：mx+4y-m-2=0，l2：x+my-m=0，实数m为何值时，l1与l2：
（1）相交；
（2）平行；
（3）重合．
已知数列{an}的前n项和，Sn=n2+2n．
（Ⅰ）求数列{an}的通项公式an；
（Ⅱ）记Tn=
1
a1a2
+
1
a2a3
+…+
1
anan+1
，求Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网