题目内容
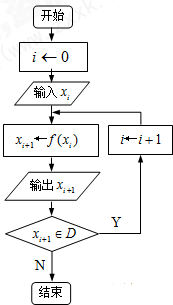 对任意函数f(x),x∈D,可按如图构造一个数列发生器,由数列发生器产生的数列记为{xn}.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,由数列发生器产生的数列记为{xn}.(1)若定义函数f(x)=
| 2x-1 |
| x+1 |
(2)若定义函数f(x)=x+3,且输入x0=-1,设Sn是数列{xn}的前n项和,对于给定的n,请你给出一个D,并求Sn.
考点:数列的求和,程序框图
专题:等差数列与等比数列
分析:(1)利用xn+1=f(xn)=xn+3,代入计算即可得出;
(2)由图可得xn+1=f(xn)=xn+3,利用等差数列的通项公式及其前n项和公式即可得出.
(2)由图可得xn+1=f(xn)=xn+3,利用等差数列的通项公式及其前n项和公式即可得出.
解答:
解:(1)∵f(x)的定义域D=(-∞,-1)∪(-1,+∞).
把x0=2代入可得x1=1;
把x1=1代入可得x2=
;
把得x2=
代入可得x3=0;
把x3=0代入可得x4=-1,
∵x4=-1∉D,
∴数列{xn}只有四项:x1=1,x2=
,x3=0,x4=-1.
(2)f(x)=x+3的定义域为R,∵x0=-1,∴x1=2,
由图可得xn+1=f(xn)=xn+3,
∴xn+1-xn=3,
∴数列{xn}是首项为2,公差为3的等差数列,
∴xn=2+3(n-1)=3n-1,
即数列{xn}的通项公式xn=3n-1,
∴D(-∞,3n-4].
数列{xn}的前n项和Sn=
=
.
把x0=2代入可得x1=1;
把x1=1代入可得x2=
| 1 |
| 2 |
把得x2=
| 1 |
| 2 |
把x3=0代入可得x4=-1,
∵x4=-1∉D,
∴数列{xn}只有四项:x1=1,x2=
| 1 |
| 2 |
(2)f(x)=x+3的定义域为R,∵x0=-1,∴x1=2,
由图可得xn+1=f(xn)=xn+3,
∴xn+1-xn=3,
∴数列{xn}是首项为2,公差为3的等差数列,
∴xn=2+3(n-1)=3n-1,
即数列{xn}的通项公式xn=3n-1,
∴D(-∞,3n-4].
数列{xn}的前n项和Sn=
| n(3n-1) |
| 2 |
| 3n2+n |
| 2 |
点评:本题考查了算法程序、等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若
<θ<π且cosθ=-
,则sin(θ+
)=( )
| π |
| 2 |
| 3 |
| 5 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
双曲线9x2-16y2=1的焦距是( )
A、
| ||
B、
| ||
C、
| ||
D、
|