题目内容
已知函数f(x)=ax+
(a>1).
(1)讨论函数f(x)的单调性;
(2)函数f(x)是否有负零点,若有,请求出负零点;若没有,请予以证明.
| x-2 |
| x+1 |
(1)讨论函数f(x)的单调性;
(2)函数f(x)是否有负零点,若有,请求出负零点;若没有,请予以证明.
考点:函数单调性的性质,函数零点的判定定理
专题:函数的性质及应用
分析:(1)先求出函数的定义域,利用导数的符号判断函数的单调性.
(2)化简函数的解析式,根据函数的单调性及最值判断函数的零点个数,从而得出结论.
(2)化简函数的解析式,根据函数的单调性及最值判断函数的零点个数,从而得出结论.
解答:
解:(1)由函数f(x)=ax+
(a>1),可得x≠-1,
故函数f(x)的定义域为(-∞,-1)∪(-1,+∞).
由于f′(x)=axlna+
,a>1,∴ax>0,lna>0,又x≠-1,
>0.
所以,当x∈(-∞,-1)时,f'(x)>0;当x∈(-1,+∞),f'(x)>0.
故函数f(x)在(-∞,-1)和(-1,+∞)上是单调递增的.
(2)函数f(x)没有负零点,原因如下:
f(x)=ax+
=ax-
+1,
当x<-1时,因为ax>0,-
>0,所以f(x)>1,故函数f(x)在(-∞,-1)上没有零点.
当-1<x<0时,因为函数f(x)在(-1,+∞)上是单调递增的,
所以,当-1<x<0时,f(x)<f(0),又f(0)=a0-
+1=-1,所以f(x)<-1.
故函数f(x)在(-1,0)上没有零点.
综上可知,函数f(x)没有负零点.
| x-2 |
| x+1 |
故函数f(x)的定义域为(-∞,-1)∪(-1,+∞).
由于f′(x)=axlna+
| 3 |
| (x+1)2 |
| 3 |
| (x+1)2 |
所以,当x∈(-∞,-1)时,f'(x)>0;当x∈(-1,+∞),f'(x)>0.
故函数f(x)在(-∞,-1)和(-1,+∞)上是单调递增的.
(2)函数f(x)没有负零点,原因如下:
f(x)=ax+
| x-2 |
| x+1 |
| 3 |
| x+1 |
当x<-1时,因为ax>0,-
| 3 |
| x+1 |
当-1<x<0时,因为函数f(x)在(-1,+∞)上是单调递增的,
所以,当-1<x<0时,f(x)<f(0),又f(0)=a0-
| 3 |
| 0+1 |
故函数f(x)在(-1,0)上没有零点.
综上可知,函数f(x)没有负零点.
点评:本题主要考查利用导数研究函数的单调性、函数的零点的判定定理,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
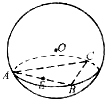 已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( )
已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( )A、
| ||
| B、2π | ||
C、
| ||
| D、3π |
函数y=(2a2-3a+2)ax是指数函数,则a的取值范围是( )
| A、a>0,a≠1 | ||
| B、0<a<1 | ||
C、a=
| ||
D、
|
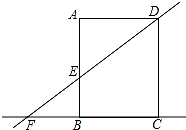 如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6.
如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6.