题目内容
已知数列{an}的首项a1=
,前n项和为Sn,且满足2an+1+Sn=3(n∈N*)
(Ⅰ)求a2及an;
(Ⅱ)求满足
<
<
的所有n的值.
| 3 |
| 2 |
(Ⅰ)求a2及an;
(Ⅱ)求满足
| 34 |
| 33 |
| S2n |
| Sn |
| 8 |
| 7 |
考点:数列递推式,数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)根据数列的递推关系,令n=1,即可求a2,构造方程组里有作差法,构造等比数列即可求an;
(Ⅱ)根据数列的递推关系求出Sn,然后代入不等式,解不等式即可.
(Ⅱ)根据数列的递推关系求出Sn,然后代入不等式,解不等式即可.
解答:
解:(Ⅰ)由2an+1+Sn=3,得2a2+a1=3,
又a1=
,
∴a2=
(3-
)=
.
由2an+1+Sn=3,2an+Sn-1=3(n≥2)相减,
得
=
,
∵
=
,
∴数列{an}是以
为首项,
以
为公比的等比数列.
因此an=
(
)n-1=3×(
)n(n∈N*).
(Ⅱ)∵2an+1+Sn=3,
∴Sn=3-2an+1=3-3×(
)n,
则由
<
<
得
<
<
,
即
<1+(
)n<
,
即
<(
)n<
∴n=3,4,5.
又a1=
| 3 |
| 2 |
∴a2=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
由2an+1+Sn=3,2an+Sn-1=3(n≥2)相减,
得
| an+1 |
| an |
| 1 |
| 2 |
∵
| a2 |
| a1 |
| 1 |
| 2 |
∴数列{an}是以
| 3 |
| 2 |
以
| 1 |
| 2 |
因此an=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)∵2an+1+Sn=3,
∴Sn=3-2an+1=3-3×(
| 1 |
| 2 |
则由
| 34 |
| 33 |
| S2n |
| Sn |
| 8 |
| 7 |
| 34 |
| 33 |
3-3(
| ||
3-3(
|
| 8 |
| 7 |
即
| 34 |
| 33 |
| 1 |
| 2 |
| 8 |
| 7 |
即
| 1 |
| 33 |
| 1 |
| 2 |
| 1 |
| 7 |
∴n=3,4,5.
点评:本题主要考查等比数列的应用,根据数列的递推关系,结合等比数列的定义求出通项公式是解决本题的关键.

练习册系列答案
相关题目
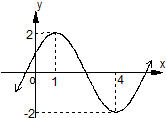 已知简谐运动f(x)=Asin(ωx+φ),(|φ|<
已知简谐运动f(x)=Asin(ωx+φ),(|φ|<| π |
| 2 |
则该简谐运动的最小正周期和初相φ分别为( )
A、T=6,φ=
| ||
B、T=6,φ=
| ||
C、T=6,φ=
| ||
D、T=6,φ=
|
在△ABC中,角A,B,C的对边分别为a,b,c,且b2+a2=c2+
ab,则内角C=( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列结论中正确的是( )
| A、偶函数的图象一定与y轴相交 |
| B、奇函数y=f(x)在x=0处有定义,则f(0)=0 |
| C、奇函数y=f(x)图象一定过原点 |
| D、图象过原点的奇函数必是单调函数 |
设集合M={x|x=
+
,k∈Z},N={x|x=
+
,k∈Z},则( )
| k |
| 2 |
| 1 |
| 2 |
| k |
| 4 |
| 1 |
| 2 |
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |
 已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).
已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).