题目内容
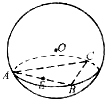已知正△ABC三个顶点都在半径为2的球面上，球心O到平面ABC的距离为1，点E是线段AB的中点，过点E作球O的截面，则截面面积的最小值是（ ）A、
| ||
| B、2π | ||
C、
| ||
| D、3π |
考点：球的体积和表面积
专题：空间位置关系与距离
分析：设正△ABC的中心为O1，连结O1A．根据球的截面圆性质、正三角形的性质与勾股定理，而经过点E的球O的截面，当截面与OE垂直时截面圆的半径最小，相应地截面圆的面积有最小值，由此算出截面圆半径的最小值，从而可得截面面积的最小值．
解答：
解：设正△ABC的中心为O1，连结O1A
∵O1是正△ABC的中心，A、B、C三点都在球面上，
∴O1O⊥平面ABC，∵球的半径R=2，球心O到平面ABC的距离为1，得O1O=1，
∴Rt△O1OA中，O1A=
=
．
又∵E为BC的中点，△ABC是等边三角形，∴AE=AO1cos30°=
．
∵过E作球O的截面，当截面与OE垂直时，截面圆的半径最小，
∴当截面与OE垂直时，截面圆的面积有最小值．
此时截面圆的半径r=
，
可得截面面积为S=πr2=
．
故选C．
∵O1是正△ABC的中心，A、B、C三点都在球面上，
∴O1O⊥平面ABC，∵球的半径R=2，球心O到平面ABC的距离为1，得O1O=1，
∴Rt△O1OA中，O1A=
| OA2-OO12 |
| 3 |
又∵E为BC的中点，△ABC是等边三角形，∴AE=AO1cos30°=
| 3 |
| 2 |
∵过E作球O的截面，当截面与OE垂直时，截面圆的半径最小，
∴当截面与OE垂直时，截面圆的面积有最小值．
此时截面圆的半径r=
| 3 |
| 2 |
可得截面面积为S=πr2=
| 9π |
| 4 |
故选C．
点评：本题已知球的内接正三角形与球心的距离，求经过正三角形中点的最小截面圆的面积．着重考查了勾股定理、球的截面圆性质与正三角形的性质等知识，属于中档题．
练习册系列答案
相关题目
在△ABC中，角A，B，C的对边分别为a，b，c，且b2+a2=c2+
ab，则内角C=（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f（x）是定义域为R的偶函数，当x≥0时，f（x）=x（2-x）．设集合M={x|x=
+
，k∈Z}，N={x|x=
+
，k∈Z}，则（ ）
| k |
| 2 |
| 1 |
| 2 |
| k |
| 4 |
| 1 |
| 2 |
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |
某项公益活动需要从3名学生会干部和2名非学生会干部中选出3人参加，则所选的3个人中至少有1个是非学生会干部的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
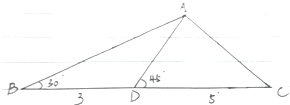在△ABC中，BD=3，DC=5，∠B=30°，∠ADC═45° 求AC．