题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,过椭圆顶点(a,0),(0,b)的直线与圆x2+y2=
相切.
(1)求椭圆C的方程;
(2)若过点 M(2,0)的直线与椭圆C相交于两点 A,B,设 P为椭圆上一点,且满足
+
=t
( O为坐标原点),当|
-
|<
时,求实数t的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
| 3 |
(1)求椭圆C的方程;
(2)若过点 M(2,0)的直线与椭圆C相交于两点 A,B,设 P为椭圆上一点,且满足
| OA |
| OB |
| OP |
| PA |
| PB |
2
| ||
| 3 |
考点:直线与圆锥曲线的综合问题,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意知e=
=
,利用a2=b2+c2,可得a2=2b2;由于过椭圆顶点(a,0),(0,b)的直线bx+ay-ab=0与圆x2+y2=
相切,
可得
=
,联立解得即可.
(2)由题意知直线AB的斜率存在.设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),与椭圆方程联立可得△>0,及其根与系数的关系,再利用向量坐标运算、弦长公式、点与椭圆的位置关系即可得出.
| c |
| a |
| ||
| 2 |
| 2 |
| 3 |
可得
| |ab| | ||
|
|
(2)由题意知直线AB的斜率存在.设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),与椭圆方程联立可得△>0,及其根与系数的关系,再利用向量坐标运算、弦长公式、点与椭圆的位置关系即可得出.
解答:
解:(1)由题意知e=
=
,
∴e2=
=
=
.即a2=2b2,①
∵过椭圆顶点(a,0),(0,b)的直线bx+ay-ab=0与圆x2+y2=
相切,
∴
=
,②
由①②联立解得a2=2,b2=1,
故椭圆C的方程为
+y2=1.
(2)由题意知直线AB的斜率存在.设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),
由
得(1+2k2)x2-8k2x+8k2-2=0.
△=64k4-4(2k2+1)(8k2-2)>0,可得k2<
,
∴x1+x2=
,x1•x2=
.
∵
+
=t
( O为坐标原点),
∴(x1+x2,y1+y2)=(tx,ty),
∴(x,y)=(
,
),
y1+y2=k(x1+x2-4)=
.
∵点P在椭圆上,∴
+2
=2,
∴16k2=t2(1+2k2),
∵|
-
|<
,
∴
|x1-x2|<
,
(1+k2)[(x1+x2)2-4x1•x2]<
,
∴(1+k2)[
-4×
]<
,
∴(4k2-1)(14k2+13)>0,
∴k2>
,
∴
<k2<
,
∵16k2=t2(1+2k2),
∴t2=
=8-
,
∴-2<t<-
或
<t<2,
∴实数取值范围为(-2,-
)∪(
,2).
| c |
| a |
| ||
| 2 |
∴e2=
| c2 |
| a2 |
| a2-b2 |
| a2 |
| 1 |
| 2 |
∵过椭圆顶点(a,0),(0,b)的直线bx+ay-ab=0与圆x2+y2=
| 2 |
| 3 |
∴
| |ab| | ||
|
|
由①②联立解得a2=2,b2=1,
故椭圆C的方程为
| x2 |
| 2 |
(2)由题意知直线AB的斜率存在.设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),
由
|
△=64k4-4(2k2+1)(8k2-2)>0,可得k2<
| 1 |
| 2 |
∴x1+x2=
| 8k2 |
| 1+2k2 |
| 8k2-2 |
| 1+2k2 |
∵
| OA |
| OB |
| OP |
∴(x1+x2,y1+y2)=(tx,ty),
∴(x,y)=(
| x1+x2 |
| t |
| y1+y2 |
| t |
y1+y2=k(x1+x2-4)=
| -4k |
| 1+2k2 |
∵点P在椭圆上,∴
| (8k2)2 |
| t2(1+2k2)2 |
| (-4k)2 |
| t2(1+2k2)2 |
∴16k2=t2(1+2k2),
∵|
| PA |
| PB |
2
| ||
| 3 |
∴
| 1+k2 |
2
| ||
| 3 |
(1+k2)[(x1+x2)2-4x1•x2]<
| 20 |
| 9 |
∴(1+k2)[
| 64k4 |
| (1+2k2)2 |
| 8k2-2 |
| 1+2k2 |
| 20 |
| 9 |
∴(4k2-1)(14k2+13)>0,
∴k2>
| 1 |
| 4 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
∵16k2=t2(1+2k2),
∴t2=
| 16k2 |
| 1+2k2 |
| 8 |
| 1+2k2 |
∴-2<t<-
2
| ||
| 3 |
2
| ||
| 3 |
∴实数取值范围为(-2,-
2
| ||
| 3 |
2
| ||
| 3 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得△>0及根与系数的关系、向量坐标运算、弦长公式、点与椭圆的位置关系,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合M={x|x=
+
,k∈Z},N={x|x=
+
,k∈Z},则( )
| k |
| 2 |
| 1 |
| 2 |
| k |
| 4 |
| 1 |
| 2 |
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |
已知A(x1,y1),B(x2,y2)是直线ax+by+c=0(b≠0)上两点,则|AB|等于( )
A、
| ||||
B、|
| ||||
C、|x1-x2|•
| ||||
D、|
|
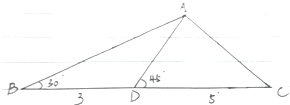 在△ABC中,BD=3,DC=5,∠B=30°,∠ADC═45° 求AC.
在△ABC中,BD=3,DC=5,∠B=30°,∠ADC═45° 求AC.