题目内容
已知公差大于零的等差数列{an}满足a1,a3,a5+18成等比数列,且第5到第9项之间的和是100.
(1)求数列{an}的通项公式;
(2)设bn=
,若数列{
}的前n项和为Sn,求
的最大值.
(1)求数列{an}的通项公式;
(2)设bn=
| an+4 |
| 3 |
| 1 |
| bnbn+1 |
| Sn |
| n+2 |
考点:数列的求和,等差数列的通项公式
专题:等差数列与等比数列
分析:(1)利用等差数列与等比数列的通项公式即可得出;
(2)利用“裂项求和”、基本不等式的性质即可得出.
(2)利用“裂项求和”、基本不等式的性质即可得出.
解答:
解:(1)设等差数列{an}的公差为d,
∵a1,a3,a5+18成等比数列,且第5到第9项之间的和是100.
∴(a1+2d)2=a1•(a5+18),a5+a6+a7+a8+a9=100,
∴(a1+2d)2=a1(a1+4d+18),5a1+30d=100,
解得a1=2,d=3.
∴an=2+3(n-1)=3n-1.
(2)bn=
=n+1,
∴
=
=
-
,
其前n项和为Sn=(
-
)+(
-
)+…+(
-
)=
-
=
.
∴
=
=
≤
=
,当且仅当n=2时取等号.
∴
的最大值是
.
∵a1,a3,a5+18成等比数列,且第5到第9项之间的和是100.
∴(a1+2d)2=a1•(a5+18),a5+a6+a7+a8+a9=100,
∴(a1+2d)2=a1(a1+4d+18),5a1+30d=100,
解得a1=2,d=3.
∴an=2+3(n-1)=3n-1.
(2)bn=
| an+4 |
| 3 |
∴
| 1 |
| bnbn+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
其前n项和为Sn=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
| n |
| 2(n+2) |
∴
| Sn |
| n+2 |
| n |
| 2(n+2)2 |
| 1 | ||
2n+
|
| 1 | ||||
2
|
| 1 |
| 12 |
∴
| Sn |
| n+2 |
| 1 |
| 12 |
点评:本题考查了等差数列与等比数列的通项公式、“裂项求和”、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
阅读如图所示的程序图,运行相应的程序输出的结果s=( )


| A、1 | B、4 | C、9 | D、16 |
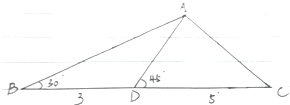 在△ABC中,BD=3,DC=5,∠B=30°,∠ADC═45° 求AC.
在△ABC中,BD=3,DC=5,∠B=30°,∠ADC═45° 求AC.