题目内容
已知在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,且满足4cosC+cos2C=4cosCcos2
.
(1)求∠C的大小;
(2)若|
-
|=2,求△ABC面积的最大值.
| C |
| 2 |
(1)求∠C的大小;
(2)若|
| CA |
| 1 |
| 2 |
| CB |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:解三角形
分析:(1)利用二倍角公式对原等式化简可求得cosC的值,进而求得C.
(2)对原等式平方,利用向量的数量积的运算公式求得关于a和b的关系式,进而利用基本不等式求得ab的范围,进而求得三角形面积的最大值.
(2)对原等式平方,利用向量的数量积的运算公式求得关于a和b的关系式,进而利用基本不等式求得ab的范围,进而求得三角形面积的最大值.
解答:
解:(1)∵4cosC+cos2C=4cosCcos2
,
∴cosC=
,
由C为三角形的内角,则C=
.
(2)∵|
-
|=2,
∴(|
-
|)2=4,
即
2+
2-
•
=4,
即b2+
a2-
ab=4,
∵b2+
a2≥ab,
∴4+
ab≥ab,
ab≤8,当且仅当b=
a时等号成立.
则△ABC的面积S=
absinC≤2
.
则三角形ABC的面积的最大值为2
.
| C |
| 2 |
∴cosC=
| 1 |
| 2 |
由C为三角形的内角,则C=
| π |
| 3 |
(2)∵|
| CA |
| 1 |
| 2 |
| CB |
∴(|
| CA |
| 1 |
| 2 |
| CB |
即
| CA |
| 1 |
| 4 |
| AB |
| CA |
| CB |
即b2+
| 1 |
| 4 |
| 1 |
| 2 |
∵b2+
| 1 |
| 4 |
∴4+
| 1 |
| 2 |
ab≤8,当且仅当b=
| 1 |
| 2 |
则△ABC的面积S=
| 1 |
| 2 |
| 3 |
则三角形ABC的面积的最大值为2
| 3 |
点评:本题主要考查了三角函数恒等变换的应用,平面向量的数量积的运算的应用.考查了学生计算能力和变通能力.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
某项公益活动需要从3名学生会干部和2名非学生会干部中选出3人参加,则所选的3个人中至少有1个是非学生会干部的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知A(x1,y1),B(x2,y2)是直线ax+by+c=0(b≠0)上两点,则|AB|等于( )
A、
| ||||
B、|
| ||||
C、|x1-x2|•
| ||||
D、|
|
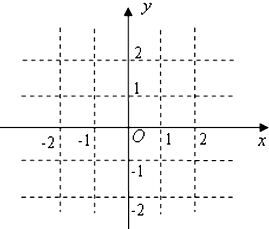 已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).
已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).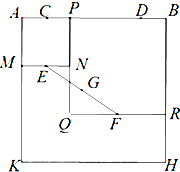 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为
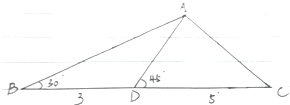 在△ABC中,BD=3,DC=5,∠B=30°,∠ADC═45° 求AC.
在△ABC中,BD=3,DC=5,∠B=30°,∠ADC═45° 求AC.