题目内容
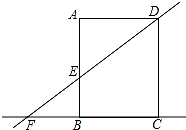 如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6.
如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6.(1)若点P是边AD上的一个动点(不与点A、D重合),PH⊥DE于H,设DP为x,四边形AEHP的面积为y,试求y与x的函数解析式;
(2)若AE=2EB.
①求圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长;
②半径为4,圆心在直线DF上,且与矩形ABCD的至少一边所在直线相切的圆共有多少个?(直接写出满足条件的圆的个数即可)
考点:圆方程的综合应用
专题:综合题,直线与圆
分析:(1)根据题意,作PH⊥DF于点H,进而得出△PHD∽△EAD,即可求出DH=
x,PH=
x,利用y=S△AED-S△PHD求出即可;
(2)①分别利用若⊙O1与直线DE、AB都相切,且圆心O1在AB的左侧,过点O1作O1G1⊥DF于G1,若⊙O2与直线DE、AB都相切,且圆心O2在AB的右侧,过点O2作O2G2⊥DF于G2,求出即可;
②利用图形分析得出所有的可能即可.
| 4 |
| 5 |
| 3 |
| 5 |
(2)①分别利用若⊙O1与直线DE、AB都相切,且圆心O1在AB的左侧,过点O1作O1G1⊥DF于G1,若⊙O2与直线DE、AB都相切,且圆心O2在AB的右侧,过点O2作O2G2⊥DF于G2,求出即可;
②利用图形分析得出所有的可能即可.
解答:
解:(1)如图1,作PH⊥DF于点H,
在Rt△AED中,
∵AE=6,AD=8,
∴ED=10,
∵∠PHD=∠EAD=90°,∠PDH=∠EDA,
∴△PHD∽△EAD,
∴
=
=
,
∴DH=
x,PH=
x,
∴y=S△AED-S△PHD=24-
x2;
(2)①∵∥BC,
∴△EBF∽△EAD,
∴
=
=
,
∴EF=5,BF=4,
如图1,若⊙O1与直线DE、AB都相切,且圆心O1在AB的左侧,过点O1作O1G1⊥DF于G1,
则可设O1G1=O1B=r1,
∵S△EO1F+S△EBO1=S△EBF,
∴
r1×5+
r1×3=
×3×4,
解得:r1=
,
若⊙O2与直线DE、AB都相切,且圆心O2在AB的右侧,过点O2作O2G2⊥DF于G2,
则可设O2G2=O2B=r2,
∵S△FO2D=
FO2×DC=
DF×O2G2,
∴
×(4+r2)×(6+3)=
×(10+5)×r2,
解得:r2=6,
即满足条件的圆的半径为
或6;
②如图2所示:符合题意的有7个.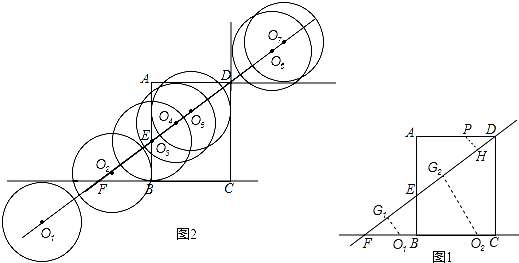
在Rt△AED中,
∵AE=6,AD=8,
∴ED=10,
∵∠PHD=∠EAD=90°,∠PDH=∠EDA,
∴△PHD∽△EAD,
∴
| x |
| 10 |
| DH |
| 8 |
| PH |
| 6 |
∴DH=
| 4 |
| 5 |
| 3 |
| 5 |
∴y=S△AED-S△PHD=24-
| 6 |
| 25 |
(2)①∵∥BC,
∴△EBF∽△EAD,
∴
| EF |
| 10 |
| 3 |
| 6 |
| BF |
| 8 |
∴EF=5,BF=4,
如图1,若⊙O1与直线DE、AB都相切,且圆心O1在AB的左侧,过点O1作O1G1⊥DF于G1,
则可设O1G1=O1B=r1,
∵S△EO1F+S△EBO1=S△EBF,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:r1=
| 3 |
| 2 |
若⊙O2与直线DE、AB都相切,且圆心O2在AB的右侧,过点O2作O2G2⊥DF于G2,
则可设O2G2=O2B=r2,
∵S△FO2D=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得:r2=6,
即满足条件的圆的半径为
| 3 |
| 2 |
②如图2所示:符合题意的有7个.

点评:此题主要考查了圆的综合应用以及切线的性质以及相似三角形的判定与性质等知识,利用分类讨论得出是解题关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知A(x1,y1),B(x2,y2)是直线ax+by+c=0(b≠0)上两点,则|AB|等于( )
A、
| ||||
B、|
| ||||
C、|x1-x2|•
| ||||
D、|
|
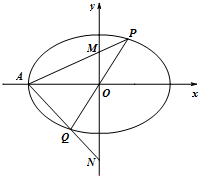 如图,在平面直角坐标系xOy中,离心率为
如图,在平面直角坐标系xOy中,离心率为