题目内容
设定义在R上的函数f(x)是最小正周期为2π的偶函数,f′(x)是f(x)的导函数,当x∈[0,π]时;0<f(x)<2;当x∈(0,π)且x≠
时,(x-
)f′(x)>0,则函数y=f(x)-|tanx|在区间[-2π,2π]上的零点个数为( )
| π |
| 2 |
| π |
| 2 |
| A、2 | B、4 | C、6 | D、8 |
考点:根的存在性及根的个数判断,导数的运算
专题:函数的性质及应用
分析:根据导数研究函数的单调性,利用函数的奇偶性和周期性,作出两个函数的图象,即可判断函数零点的个数.
解答:
解:∵当x∈(0,π)且x≠
时,(x-
)f′(x)>0,
∴当
<x<π时,f'(x)>0,函数f(x)单调递增,
当0<x<
时,f'(x)<0,函数f(x)单调递减,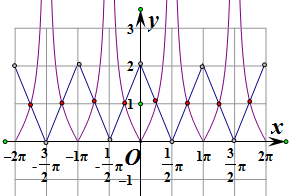
由y=f(x)-|tanx|=0得f(x)=|tanx|,
∵f(x)是最小正周期为2π的偶函数,
∴作出函数y=f(x)和y=|tanx|在区间[-2π,2π]上的图象如图:
则两个函数图象有8个交点,
即函数数y=f(x)-|tanx|在区间[-2π,2π]上的零点个数为8个,
故选:D.
| π |
| 2 |
| π |
| 2 |
∴当
| π |
| 2 |
当0<x<
| π |
| 2 |

由y=f(x)-|tanx|=0得f(x)=|tanx|,
∵f(x)是最小正周期为2π的偶函数,
∴作出函数y=f(x)和y=|tanx|在区间[-2π,2π]上的图象如图:
则两个函数图象有8个交点,
即函数数y=f(x)-|tanx|在区间[-2π,2π]上的零点个数为8个,
故选:D.
点评:本题主要考查函数零点个数的判断,利用函数的奇偶性和周期性的性质是解决本题的关键,综合考查函数性质的应用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
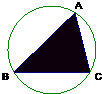 如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )
如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={x|(
)x<1},B={x|x2-3x-4>0},则A∩B等于( )
| 1 |
| 2 |
| A、{x|x>0} |
| B、{x|x<-1或x>0} |
| C、{x|x>4} |
| D、{x|-1≤x≤4} |
已知函数y=f(x),数列{an}的通项公式是an=f(n),n∈N*,那么“函数y=f(x)在[1,+∞﹚上单调递增”是“数列{an}是递增数列”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知函数f(x)是定义在R上的偶函数,它在[0,+∞)上是减函数.则下列各式一定成立的是( )
| A、f(0)<f(6) |
| B、f(-3)>f(2) |
| C、f(-1)>f(3) |
| D、f(-2)<f(-3) |
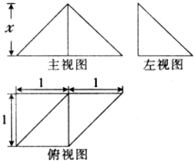 如图所示是一个几何体的三视图,若该几何体的体积为
如图所示是一个几何体的三视图,若该几何体的体积为| 1 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
 在平面直角坐标系xoy中,如图,已知椭圆
在平面直角坐标系xoy中,如图,已知椭圆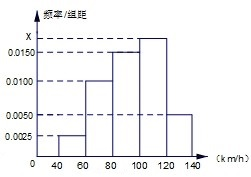 根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有
根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有