题目内容
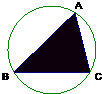 如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )
如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:几何概型
专题:概率与统计
分析:根据正弦定理求出相应的边长,利用三角形的面积公式求出阴影部分的面积,结合几何概型的概率公式即可得到结论.
解答:
解:∵圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,
∴根据正弦定理可知
=
=2R,
即AC=2RsinB=2×10×
=10
,BC=2RsinA=2×10×
=10
,
∴sinC=sin(180°-60°-45°)=sin(60°+45°)=
(
+
),
∴△ABC的面积S=
AC•BC•sinC=
×10
×10
×
×(
+
)=25(3+
),
则圆的面积为π×102=100π,
根据几何概型的概率公式可知豆子落在三角形ABC内的概率为
=
,
故选:B.
∴根据正弦定理可知
| AC |
| sinB |
| BC |
| sinA |
即AC=2RsinB=2×10×
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
∴sinC=sin(180°-60°-45°)=sin(60°+45°)=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
则圆的面积为π×102=100π,
根据几何概型的概率公式可知豆子落在三角形ABC内的概率为
25(3+
| ||
| 100π |
3+
| ||
| 4π |
故选:B.
点评:本题主要考查几何概型的概率计算,根据正弦定理求出三角形的边长和面积是解决本题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
已知
=(1,2),
=(3,4),则向量
在
方向上的投影为( )
| a |
| b |
| b |
| a |
| A、5 | ||||
B、
| ||||
| C、3 | ||||
D、
|
某几何体的三视图如图所示,则该几何体的体积为( )


| A、6 | ||
B、2
| ||
| C、3 | ||
D、3
|
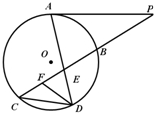 如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=