题目内容
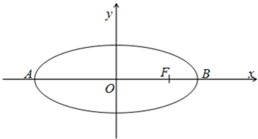 在平面直角坐标系xoy中,如图,已知椭圆
在平面直角坐标系xoy中,如图,已知椭圆| x2 |
| 9 |
| y2 |
| 5 |
(1)设动点P满足(
| PF |
| PB |
| PF |
| PB |
(2)设x1=2,x2=
| 1 |
| 3 |
(3)若点T在点P的轨迹上运动,问直线MN是否经过x轴上的一定点,若是,求出定点的坐标;若不是,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)利用椭圆的标准方程可得F,B,再利用数量积运算即可得出;
(2)由x1=2,x2=
,代入椭圆的方程可得y1,y2,进而得到直线TM、TN的方程,联立即可得出交点T的坐标;
(3)假设直线MN过定点,由T在点P的轨迹上,可得T(9,m),分别得出直线AT、BT的方程,与椭圆的方程联立可得点M,N的坐标,得出直线MN的方程即可.
(2)由x1=2,x2=
| 1 |
| 3 |
(3)假设直线MN过定点,由T在点P的轨迹上,可得T(9,m),分别得出直线AT、BT的方程,与椭圆的方程联立可得点M,N的坐标,得出直线MN的方程即可.
解答:
解:(1)由椭圆
+
=1可得:a2=9,b2=5,c=
=2.
∴F(2,0),B(3,0).
设P(x,y),则
=(2-x,-y),
=(3-x,-y).
∵满足(
+
)•(
-
)=13,
∴(5-2x,-2y)•(-1,0)=13,
∴2x-5=13,
化简得x=9,
故P的轨迹方程为x=9
(2)由x1=2,
+
=1及y1>0得y1=
,则点M(2,
),
从而直线AM的方程为y=
x+1;
同理可以求得直线BN的方程为y=
x-
联立两方程可解得x=7,y=
∴点T的坐标为(7,
).
(3)假设直线MN过定点,由T在点P的轨迹上,T(9,m)
直线AT的方程为y=
(x+3),直线BT的方程为y=
(x-3)
点M(x1,y1)满足
得
=-
•
,
又x1≠3,解得x1=
,从而得y1=
.
同理:x2=
,y2=
.
∴直线MN的方程:y+
=
(x-
),
| x2 |
| 9 |
| y2 |
| 5 |
| 9-5 |
∴F(2,0),B(3,0).
设P(x,y),则
| PF |
| PB |
∵满足(
| PF |
| PB |
| PF |
| PB |
∴(5-2x,-2y)•(-1,0)=13,
∴2x-5=13,
化简得x=9,
故P的轨迹方程为x=9
(2)由x1=2,
| ||
| 9 |
| ||
| 5 |
| 5 |
| 3 |
| 5 |
| 3 |
从而直线AM的方程为y=
| 1 |
| 3 |
同理可以求得直线BN的方程为y=
| 5 |
| 6 |
| 5 |
| 2 |
联立两方程可解得x=7,y=
| 10 |
| 3 |
∴点T的坐标为(7,
| 10 |
| 3 |
(3)假设直线MN过定点,由T在点P的轨迹上,T(9,m)
直线AT的方程为y=
| m |
| 12 |
| m |
| 6 |
点M(x1,y1)满足
|
| (x1-3)(x1+3) |
| 9 |
| m2 |
| 122 |
| (x1+3)2 |
| 5 |
又x1≠3,解得x1=
| 240-3m2 |
| 80+m2 |
| 40m |
| 80+m2 |
同理:x2=
| 3m2-60 |
| m2+20 |
| -20m |
| m2+20 |
∴直线MN的方程:y+
| 20m |
| m2+20 |
| 10m |
| 40-m2 |
| 3m2-60 |
| m2+20 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得出方程组、数量积运算、直线过定点问题等基础知识与基本技能方法,考查了计算能力,属于难题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
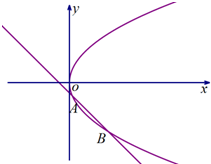 已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.
已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.