题目内容
已知集合A={x|(
)x<1},B={x|x2-3x-4>0},则A∩B等于( )
| 1 |
| 2 |
| A、{x|x>0} |
| B、{x|x<-1或x>0} |
| C、{x|x>4} |
| D、{x|-1≤x≤4} |
考点:交集及其运算
专题:集合
分析:分别求出A与B中不等式的解集确定出A与B,找出两集合的交集即可.
解答:
解:由A中的不等式变形得:(
)x<1=(
)0,
解得:x>0,即A={x|x>0},
由B中的不等式变形得:(x-4)(x+1)>0,
解得:x<-1或x>4,
∴B={x|x<-1或x>4},
则A∩B={x|x>4}.
故选:C.
| 1 |
| 2 |
| 1 |
| 2 |
解得:x>0,即A={x|x>0},
由B中的不等式变形得:(x-4)(x+1)>0,
解得:x<-1或x>4,
∴B={x|x<-1或x>4},
则A∩B={x|x>4}.
故选:C.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知不等式
>0的解集为(-1,2),则二项式(ax-
)6展开式的常数项是( )
| x-2 |
| ax-1 |
| 1 |
| x2 |
| A、-15 | B、15 | C、-5 | D、5 |
在锐角△ABC中,AB=3,AC=4,其面积S△ABC=3
,则BC=( )
| 3 |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
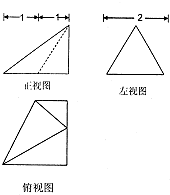 若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )
若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )| A、2cm2 | ||
B、
| ||
C、3
| ||
| D、3cm3 |
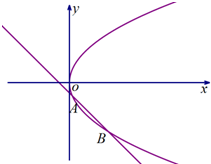 已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.
已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.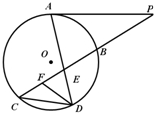 如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=