题目内容
已知二次函数f(x)=ax2+(2b+1)x-a(a,b∈R,a≠0)
(1)当a=b时,f(x)在[
,a]上有最小值
,求实数a的值;
(2)若f(x)-2在区间[1,2]上至少有一个零点,求a2+b2的最小值.
(1)当a=b时,f(x)在[
| a |
| 2 |
| 3a |
| 4 |
(2)若f(x)-2在区间[1,2]上至少有一个零点,求a2+b2的最小值.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)由给定区间可判断a的符号,进而分析出函数在区间[
,a]上的单调性,结合已知中函数的最小值,可求出满足条件的a值.
(2)令ax2+(2b+1)x-a-2=(x2-1)a+2xb+x-2=0,并将其看成为平面直角坐标系a-O-b中的一条直线,由于直线上一点(a,b)到原点的距离大于等于原点到直线的距离,构造关于a,b,x的不等式,结合对勾函数的单调性,可得a2+b2的最小值.
| a |
| 2 |
(2)令ax2+(2b+1)x-a-2=(x2-1)a+2xb+x-2=0,并将其看成为平面直角坐标系a-O-b中的一条直线,由于直线上一点(a,b)到原点的距离大于等于原点到直线的距离,构造关于a,b,x的不等式,结合对勾函数的单调性,可得a2+b2的最小值.
解答:
解:(1)∵区间[
,a]中
<a,故a>0,
当a=b时,f(x)=ax2+(2a+1)x-a的图象开口向上,对称轴为直线x=-
,
∵-
<0<
<a,
故f(x)在[
,a]上为增函数,
当x=
时,函数有最小值
,
即f(
)=
+a2-
=
,
即a(a+5)(a-1)=0,
∵a>0,
∴a=1.
(2)令ax2+(2b+1)x-a=(x2-1)a+2xb+x=0,将其看成为平面直角坐标系a-O-b中的一条直线,
由于直线上一点(a,b)到原点的距离大于等于原点到直线的距离,
即
≥
=
=
,
令g(x)=
=|
|,
则
≥g(x)max,
∵y=x-2+
在x∈[1,2)是减函数,
故g(x)=
=|
|≤g(1)=
,
故a2+b2的最小值为
.
| a |
| 2 |
| a |
| 2 |
当a=b时,f(x)=ax2+(2a+1)x-a的图象开口向上,对称轴为直线x=-
| 2a+1 |
| 2a |
∵-
| 2a+1 |
| 2a |
| a |
| 2 |
故f(x)在[
| a |
| 2 |
当x=
| a |
| 2 |
| 3a |
| 4 |
即f(
| a |
| 2 |
| a3 |
| 4 |
| a |
| 2 |
| 3a |
| 4 |
即a(a+5)(a-1)=0,
∵a>0,
∴a=1.
(2)令ax2+(2b+1)x-a=(x2-1)a+2xb+x=0,将其看成为平面直角坐标系a-O-b中的一条直线,
由于直线上一点(a,b)到原点的距离大于等于原点到直线的距离,
即
| a2+b2 |
| |x-2| | ||
|
| |x-2| | ||
|
| |x-2| |
| |x2+1| |
令g(x)=
| |x-2| |
| |x2+1| |
| 1 | ||
(x-2)+
|
则
| a2+b2 |
∵y=x-2+
| 5 |
| x-2 |
故g(x)=
| |x-2| |
| |x2+1| |
| 1 | ||
(x-2)+
|
| 1 |
| 2 |
故a2+b2的最小值为
| 1 |
| 4 |
点评:本题考查的知识点是二次函数的图象和性质,对勾函数的图象和性质,两点之间距离公式,点到直线的距离公式,是函数与解析几何的综合应用,难度较大.

练习册系列答案
相关题目
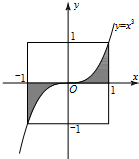 如图,设D是图中边长为2的正方形区域,E是函数y=x3的图象与x轴及x=±1围成的阴影区域.向D中随机投一点,则该点落入E中的概率为( )
如图,设D是图中边长为2的正方形区域,E是函数y=x3的图象与x轴及x=±1围成的阴影区域.向D中随机投一点,则该点落入E中的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=4,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=4,AD=2,PA=2,PD=2