题目内容
已知函数f(x)是定义在R上的偶函数,它在[0,+∞)上是减函数.则下列各式一定成立的是( )
| A、f(0)<f(6) |
| B、f(-3)>f(2) |
| C、f(-1)>f(3) |
| D、f(-2)<f(-3) |
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:由函数f(x)是偶函数,把x<0的函数值都化为x>0时的函数值,利用单调性(在[0,+∞)上是减函数)比较大小,即可判定选项A、B、C、D是否正确.
解答:
解:∵函数f(x)是定义在R上的偶函数,且在[0,+∞)上是减函数;
∴当0<6时,f(0)>f(6),∴命题A错误;
又∵f(-3)=f(3),且3>2,∴f(3)<f(2),命题B错误;
又∵f(-1)=f(1),且1<3,∴f(1)>f(3),即f(-1)>f(3),∴命题C正确;
又∵f(-2)=f(2),f(-3)=f(3),且2<3,∴f(2)>f(3),即f(-2)>f(-3),∴命题D错误;
故选:C.
∴当0<6时,f(0)>f(6),∴命题A错误;
又∵f(-3)=f(3),且3>2,∴f(3)<f(2),命题B错误;
又∵f(-1)=f(1),且1<3,∴f(1)>f(3),即f(-1)>f(3),∴命题C正确;
又∵f(-2)=f(2),f(-3)=f(3),且2<3,∴f(2)>f(3),即f(-2)>f(-3),∴命题D错误;
故选:C.
点评:本题考查了函数的奇偶性与单调性问题,解题时利用奇偶性把x<0的函数值都化为x>0时的函数值,再利用单调性比较大小.

练习册系列答案
相关题目
在锐角△ABC中,AB=3,AC=4,其面积S△ABC=3
,则BC=( )
| 3 |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
某几何体的三视图如图所示,则该几何体的体积为( )


| A、6 | ||
B、2
| ||
| C、3 | ||
D、3
|
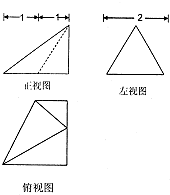 若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )
若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )| A、2cm2 | ||
B、
| ||
C、3
| ||
| D、3cm3 |
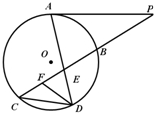 如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=