题目内容
9.已知偶函数f(x)满足f(x)=3x-3(x≥0),则不等式xf(x)<0的解集为(0,1)∪(-∞,-1).分析 先确定函数在(-∞,0)上是的解析式,再将不等式等价变形,利用函数的单调性,即可求解不等式.
解答 解:设x<0,
则-x>0,
∴f(-x)=3-x-3,
∵函数f(x)为偶函数,
∴f(-x)=f(x)=3-x-3,
∵xf(x)<0,
∴$\left\{\begin{array}{l}{x>0}\\{f(x)<0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{x>0}\\{{3}^{x}-3<0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{{3}^{-x}-3>0}\end{array}\right.$,
解得0<x<1或x<-1,
故不等式xf(x)<0的解集为(0,1)∪(-∞,-1)
故答案为:(0,1)∪(-∞,-1).
点评 本题考查函数单调性与奇偶性的结合,考查解不等式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
20.已知函数f(x)=cos($\frac{2π}{3}$x)+(a-1)sin($\frac{π}{3}$x)+a,g(x)=3x-x,若f(g(x))≤0对任意的x∈[0,1]恒成立,则实数a的取值范围是( )
| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
4.若二次函数f(x)=m2x2+nx+2的图象与x轴有交点,则双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=1$(m>0,n>0)离心率e的取值范围为( )
| A. | (1,3] | B. | [3,+∞) | C. | $(1,\frac{{3\sqrt{2}}}{4}]$ | D. | $[\frac{{3\sqrt{2}}}{4},+∞)$ |
14.在区间[-2,4]上随机地取一个数x,使${a^2}+\frac{1}{{{a^2}+1}}≥|x|$恒成立的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
 如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点M处的切线与圆C2:x2+y2=1相切于点Q.
如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点M处的切线与圆C2:x2+y2=1相切于点Q.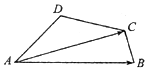 在四边形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=3.
在四边形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=3.