题目内容
20.已知函数f(x)=cos($\frac{2π}{3}$x)+(a-1)sin($\frac{π}{3}$x)+a,g(x)=3x-x,若f(g(x))≤0对任意的x∈[0,1]恒成立,则实数a的取值范围是( )| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
分析 利用导数求出函数g(x)的单调区间,得到函数在[0,1]上的值域,令t=g(x),则t∈[1,2],把问题转化为f(t)≤0对任意t∈[1,2]恒成立,即cos($\frac{2π}{3}$t)+(a-1)sin($\frac{π}{3}$t)+a≤0对任意t∈[1,2]恒成立,分离参数a,得a≤$\frac{sin\frac{π}{3}t-cos\frac{2πt}{3}}{1+sin\frac{π}{3}t}$=2sin$\frac{π}{3}t$-1,由三角函数的性质求出h(t)=2sin$\frac{π}{3}t$-1,t∈[1,2]的最小值得答案.
解答 解:g(x)=3x-x,x∈[0,1],g′(x)=3xln3-1在[0,1]上为增函数,
则g′(x)≥g′(0)=ln3-1>0,
则函数g(x)在[0,1]上单调递增,
∴g(x)在x∈[0,1]上的值域为[1,2],
令t=g(x),则t∈[1,2],
∵f[g(x)]≤0对x∈[0,1]恒成立,
∴f(t)≤0对任意t∈[1,2]恒成立,即cos($\frac{2π}{3}$t)+(a-1)sin($\frac{π}{3}$t)+a≤0对任意t∈[1,2]恒成立,
分离参数a,得a≤$\frac{sin\frac{π}{3}t-cos\frac{2πt}{3}}{1+sin\frac{π}{3}t}$=2sin$\frac{π}{3}t$-1,
令h(t)=2sin$\frac{π}{3}t$-1,t∈[1,2],
则h(t)min=2sin$\frac{π}{3}$-1=$\sqrt{3}$-1,
∴a$≤\sqrt{3}-1$,
则实数a的取值范围是(-∞,$\sqrt{3}$-1],
故选:A.
点评 本题考查了利用导数研究函数的单调性,考查利用导数求函数的最值,考查数学转化思想方法,是中档题.

| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{7}{4}$ |
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
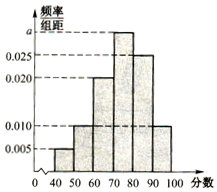 为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.
为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.