题目内容
19.已知α∈(0,$\frac{π}{2}$),若cos(α+$\frac{π}{6}$)=$\frac{3}{5}$,则sin(α-$\frac{π}{12}$)=$\frac{\sqrt{2}}{10}$.分析 由已知利用诱导公式可求sin(α-$\frac{π}{3}$),利用同角三角函数基本关系式可求cos(α-$\frac{π}{3}$)的值,进而利用两角和的正弦函数公式即可计算得解sin(α-$\frac{π}{12}$)的值.
解答 解:∵α∈(0,$\frac{π}{2}$),
∴-$\frac{π}{3}$<α-$\frac{π}{3}$<$\frac{π}{6}$,
∵cos(α+$\frac{π}{6}$)=sin($\frac{π}{3}$-α)=$\frac{3}{5}$,
∴sin(α-$\frac{π}{3}$)=-$\frac{3}{5}$,
∴cos(α-$\frac{π}{3}$)=$\sqrt{1-si{n}^{2}(α-\frac{π}{3})}$=$\frac{4}{5}$,
∴sin(α-$\frac{π}{12}$)=sin[(α-$\frac{π}{3}$)+$\frac{π}{4}$]=$\frac{\sqrt{2}}{2}$[sin(α-$\frac{π}{3}$)+cos(α-$\frac{π}{3}$)]=$\frac{\sqrt{2}}{2}$×(-$\frac{3}{5}$+$\frac{4}{5}$)=$\frac{\sqrt{2}}{10}$.
故答案为:$\frac{\sqrt{2}}{10}$.
点评 本题主要考查了诱导公式,同角三角函数基本关系式,两角和的正弦函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
9.下列函数中,与y=x相同的函数是( )
| A. | $y=\sqrt{x^2}$ | B. | y=lg10x | C. | $y=\frac{x^2}{x}$ | D. | $y={(\sqrt{x-1})^2}+1$ |
14.某4名同学(其中2男2女)报考了2017年高考英语口语考试,若有三人通过了考试,则女生甲通过考试的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
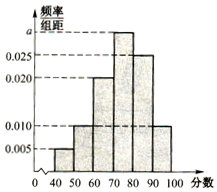 为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.
为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.