题目内容
19.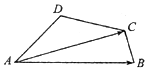 在四边形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=3.
在四边形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=3.
分析 依题意,利用余弦定理可求得|AC|=$\sqrt{3}$,继而可得∠ACB=90°,|AB|cos∠CAB=|AC|,利用平面向量数量积的定义即可求得$\overrightarrow{AB}$•$\overrightarrow{AC}$的值.
解答 解: 在三角形ADC中,∠ADC=120°,AD=DC=1,
在三角形ADC中,∠ADC=120°,AD=DC=1,
由余弦定理得:|AC|2=|AD|2+|CD|2-2|AD||CD|cos120°=1+1-2×(-$\frac{1}{2}$)=3,
故|AC|=$\sqrt{3}$,
又∠DAC=∠DCA=30°,∠BCD=120°,
所以,∠ACB=90°,即△ACB为直角三角形,
所以,|AB|cos∠CAB=|AC|,
所以$\overrightarrow{AB}$•$\overrightarrow{AC}$=|AB||AC|cos∠CAB=|AC|(|AB|cos∠CAB)=|AC|•|AC|=$\sqrt{3}$•$\sqrt{3}$=3.
故答案为:3.
点评 本题考查平面向量数量积的运算,考查余弦定理的应用与平面向量数量积的定义,属于中档题.

练习册系列答案
相关题目
10.已知圆C:x2+y2=4,直线l:y=x,则圆C上任取一点A到直线l的距离小于1的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
4.若a=ln$\frac{1}{2}$,b=($\frac{1}{3}$)0.8,c=2${\;}^{\frac{1}{3}}$,则( )
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | b<a<c |
4.已知向量$\overrightarrow{a}$=($\sqrt{3}$,-1),向量$\overrightarrow{b}$=(1+tcos$\frac{π}{5}$,tsin$\frac{π}{5}$)(t>0),则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角可能是( )
| A. | $\frac{π}{9}$ | B. | $\frac{5π}{18}$ | C. | $\frac{7π}{18}$ | D. | $\frac{11π}{18}$ |
2.某研究机构在对线性相关的两个变量x和y进行统计分析时,得到如下数据:
由表中数据求的y关于x的回归方程为$\hat y=0.65x+\hat a$,则在这些样本点中任取一点,该点落在回归直线下方的概率为( )
| x | 4 | 6 | 8 | 10 | 12 |
| y | 1 | 2 | 3 | 5 | 6 |
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
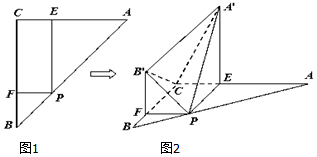 如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ>0),过点P作PE∥BC交AC于E,作PF∥AC交BC于F.沿PE将△APE翻折成△A′PE,使平面A′PE⊥平面ABC;沿PF将△BPF翻折成△B′PF,使平面B′PF⊥平面ABC.
如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ>0),过点P作PE∥BC交AC于E,作PF∥AC交BC于F.沿PE将△APE翻折成△A′PE,使平面A′PE⊥平面ABC;沿PF将△BPF翻折成△B′PF,使平面B′PF⊥平面ABC.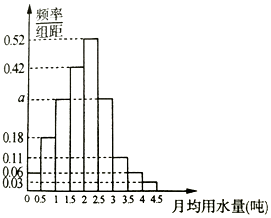 我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.