题目内容
f（x）=
，求f（x）的单调区间．
| x2-2x-3 |
考点：函数的单调性及单调区间
专题：函数的性质及应用
分析：求出函数的定义域，利用复合函数的单调性即可得到结论．
解答：
解：设t=x2-2x-3，则由t=x2-2x-3≥0得x≥3或x≤-1，
当x≥3时，函数t=x2-2x-3单调递增，
当x≤-1时，函数t=x2-2x-3单调递减，
而函数y=
单调递增，
∴由复合函数的单调性可知，
函数的递增区间为[3，+∞），
单调递减区间为（-∞，-1]．
当x≥3时，函数t=x2-2x-3单调递增，
当x≤-1时，函数t=x2-2x-3单调递减，
而函数y=
| t |
∴由复合函数的单调性可知，
函数的递增区间为[3，+∞），
单调递减区间为（-∞，-1]．
点评：本题主要考查函数单调性和单调区间的判断，利用复合函数的单调性的性质是解决本题的关键，注意要先求函数的定义域．
练习册系列答案
阅读快车系列答案
相关题目
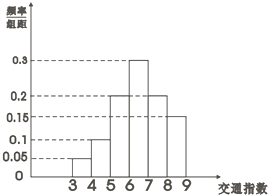交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为T．其范围为[0，10]，分别有五个级别：T∈[0，2）畅通；T∈[2，4）基本畅通； T∈[4，6）轻度拥堵； T∈[6，8）中度拥堵；T∈[8，10]严重拥堵，晚高峰时段，从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制直方图如图所示．