题目内容
化简：
（1）sin75°cos34°+sin15°cos56°
（2）cos（
-α）sinα+cos（
+α）cosα
（1）sin75°cos34°+sin15°cos56°
（2）cos（
| π |
| 6 |
| π |
| 3 |
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：利用两角和差的正弦公式、诱导公式即可得出．
解答：
解：（1）原式=sin75°cos34°+cos75°sin34°=sin（75°+34°）=sin71°．
（2）原式=sinαcos(
-α)+cosαsin(
-α)=sin(α+
-α)=sin
=
．
（2）原式=sinαcos(
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
点评：本题考查了两角和差的正弦公式、诱导公式，属于基础题．
练习册系列答案
相关题目
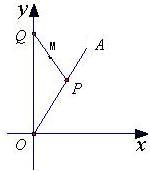如图，在平面直角坐标系xOy中，射线OA的方程为y=