题目内容
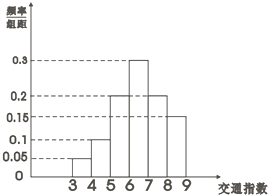 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段,从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制直方图如图所示.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段,从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制直方图如图所示.(Ⅰ)这20个路段轻度拥堵、中度拥堵的路段各有多少个?
(Ⅱ)从这20个路段中随机抽出的3个路段,用X表示抽取的中度拥堵的路段的个数,求X的分布列及期望.
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(Ⅰ)由频率分布直方图可知底×高频率,频率×20=个;由频率分布直方图很容易知道轻度拥堵的频率是0.3,中度拥堵的频率是0.5.
(Ⅱ)由题意知X为0,1,2,3,列出超几何分布的概率形式P(X=k)=
(k=0,1,2,3),再列表求值,由此求出X的分布列及期望.
(Ⅱ)由题意知X为0,1,2,3,列出超几何分布的概率形式P(X=k)=
| ||||
|
解答:
解:(Ⅰ)由直方图得:
轻度拥堵的路段落个数是(0.1+0.2)×1×20=6个,
中度拥堵的路段落个数是(0.3+0.2)×1×20=10个.
(Ⅱ)由题意知X的可能取值为0,1,2,3,
P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
,
P(X=3)=
=
,
∴X的分布列为:
EX=0×
+1×
+2×
+3×
=
.
轻度拥堵的路段落个数是(0.1+0.2)×1×20=6个,
中度拥堵的路段落个数是(0.3+0.2)×1×20=10个.
(Ⅱ)由题意知X的可能取值为0,1,2,3,
P(X=0)=
| ||||
|
| 2 |
| 19 |
P(X=1)=
| ||||
|
| 15 |
| 38 |
P(X=2)=
| ||||
|
| 15 |
| 38 |
P(X=3)=
| ||||
|
| 2 |
| 19 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 2 |
| 19 |
| 15 |
| 38 |
| 15 |
| 38 |
| 2 |
| 19 |
| 3 |
| 2 |
点评:本题考查频率分布直方图的应用,考查超几何分布,考查离散型随机变量的分布列的求法及数学期望,是中档题.

练习册系列答案
相关题目
集合A={x|1<x<2},B={x|x≥a},满足A∩B=∅,则实数a的取值范围是( )
| A、{a|a≥2} |
| B、{a|a>2} |
| C、{a|a≥1} |
| D、{a|a>1} |
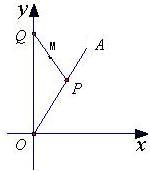 如图,在平面直角坐标系xOy中,射线OA的方程为y=
如图,在平面直角坐标系xOy中,射线OA的方程为y=