题目内容
点P(1,2,z)到点A(1,1,2)、B(2,1,1)的距离相等,则z等于( )
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
考点:空间两点间的距离公式
专题:空间位置关系与距离
分析:利用已知条件列出方程求解即可.
解答:
解:点P(1,2,z)到点A(1,1,2)、B(2,1,1)的距离相等,
∴
=
,
即
=
,
解得z=1.
故选:C.
∴
| (1-1)2+(2-1)2+(z-2)2 |
| (1-2)2+(2-1)2+(z-1)2 |
即
| 1+(z-2)2 |
| 2+(z-1)2 |
解得z=1.
故选:C.
点评:本题考查空间两点间距离公式的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设f(n)=1+
+
+…+
(n>2,n∈N),经计算可得f(4)>2,f(8)>
,f(16)>3,f(32)>
.观察上述结果,可得出的一般结论是( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 5 |
| 2 |
| 7 |
| 2 |
A、f(2n)>
| ||
B、f(n2)≥
| ||
C、f(2n)>
| ||
D、f(2n)≥
|
函数y=2sin(
x+
)的最小正周期是( )
| 1 |
| 2 |
| π |
| 3 |
| A、π | B、2π | C、-4π | D、4π |
在△ABC中,a,b,c分别为角A,B,C所对的边,且b2+c2-
bc=3,cosB=
,a=
,则边c的值为( )
| 2 |
| 4 |
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
顶点在原点,对称轴是y轴,并且顶点与焦点的距离为3的抛物线的标准方程为( )
| A、x2=±3y |
| B、y2=±6x |
| C、x2=±12y |
| D、x2=±6y |
“x>
”是“sinx>
”的( )
| π |
| 6 |
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
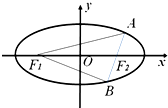 已知F1,F2为椭圆的两个焦点,|F1F2|=6,如图△AF1B的顶点A、B在椭圆上,F2在边AB上,其周长为20,则椭圆的离心率为( )
已知F1,F2为椭圆的两个焦点,|F1F2|=6,如图△AF1B的顶点A、B在椭圆上,F2在边AB上,其周长为20,则椭圆的离心率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
设a=∫
(sinx+cosx)dx,则二项式(a
-
)6展开式中各项系数之和是( )
π 0 |
| x |
| 1 | ||
|
| A、1 | B、-1 | C、2 | D、0 |