题目内容
在△ABC中,a,b,c分别为角A,B,C所对的边,且b2+c2-
bc=3,cosB=
,a=
,则边c的值为( )
| 2 |
| 4 |
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:余弦定理
专题:计算题,解三角形
分析:由b2+c2-
bc=3=a2,得b2+c2-a2=
bc,由余弦定理可求得cosA=
,由此可知A=45°,由诱导公式及和角公式可求sinC,再用正弦定理即可求得c.
| 2 |
| 2 |
| ||
| 2 |
解答:
解:∵a=
,∴b2+c2-
bc=3=a2,
则b2+c2-a2=
bc,
∴cosA=
=
=
,
又A为三角形的内角,∴A=45°,
sinC=sin(A+B)=sinAcosB+cosAsinB=
×
+
×
=
,
由正弦定理,得
=
,即
=
,
∴c=
,
故选A.
| 3 |
| 2 |
则b2+c2-a2=
| 2 |
∴cosA=
| b2+c2-a2 |
| 2bc |
| ||
| 2bc |
| ||
| 2 |
又A为三角形的内角,∴A=45°,
sinC=sin(A+B)=sinAcosB+cosAsinB=
| ||
| 2 |
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
7
| ||
| 10 |
由正弦定理,得
| a |
| sinA |
| c |
| sinC |
| ||
| sin45° |
| c | ||||
|
∴c=
7
| ||
| 5 |
故选A.
点评:本题考查解三角形、正弦定理及余弦定理,考查学生的运算求解能力.

练习册系列答案
相关题目
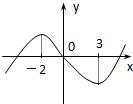 函数f(x)=x3+bx2+cx+d,图象如图,则函数y=log2(x2+
函数f(x)=x3+bx2+cx+d,图象如图,则函数y=log2(x2+| 2 |
| 3 |
| c |
| 3 |
A、[
| ||
| B、[3,+∞) | ||
| C、[-2,3] | ||
| D、(-∞,-2) |
设某种植物由出生算起长到1m的概率为0.8,长到2m的概率为0.4,现有一个1m的这种植物,它能长到2m的概率是( )
| A、0.32 | B、0.4 |
| C、0.5 | D、0.8 |
已知角α的终边经过点P(3t,-4t)(t≠0),则sinα+cosα的值为( )
A、
| ||
B、
| ||
C、-
| ||
D、±
|
点P(1,2,z)到点A(1,1,2)、B(2,1,1)的距离相等,则z等于( )
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
下列式子中,表示残差平方和的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
如图程序执行后输出的结果是( )


| A、1 | B、2 | C、3 | D、4 |
在三角形△ABC所在的平面上有一点P,满足6
=3
+2
,则△PBC与△ABC的面积之比是( )
| AP |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|

