题目内容
设f(n)=1+
+
+…+
(n>2,n∈N),经计算可得f(4)>2,f(8)>
,f(16)>3,f(32)>
.观察上述结果,可得出的一般结论是( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 5 |
| 2 |
| 7 |
| 2 |
A、f(2n)>
| ||
B、f(n2)≥
| ||
C、f(2n)>
| ||
D、f(2n)≥
|
考点:归纳推理
专题:规律型
分析:已知的式子可化为f(22)>
,f(23)>
,f(24)>
,f(25)>
,由此规律可得f(2n)≥
.
| 2+2 |
| 2 |
| 3+2 |
| 2 |
| 4+2 |
| 2 |
| 5+2 |
| 2 |
| n+2 |
| 2 |
解答:
解:已知的式子f(4)>2,
f(8)>
,
f(16)>3,
f(32)>
,
…
可化为:f(22)>
,
f(23)>
,
f(24)>
,
f(25)>
,
…
以此类推,可得f(2n)≥
,
故选:C
f(8)>
| 5 |
| 2 |
f(16)>3,
f(32)>
| 7 |
| 2 |
…
可化为:f(22)>
| 2+2 |
| 2 |
f(23)>
| 3+2 |
| 2 |
f(24)>
| 4+2 |
| 2 |
f(25)>
| 5+2 |
| 2 |
…
以此类推,可得f(2n)≥
| n+2 |
| 2 |
故选:C
点评:本题考查归纳推理,把已知的式子变形找规律是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,直线l是曲线y=f(x)在x=4处的切线,则f′(4)=( )
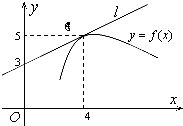

A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
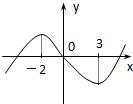 函数f(x)=x3+bx2+cx+d,图象如图,则函数y=log2(x2+
函数f(x)=x3+bx2+cx+d,图象如图,则函数y=log2(x2+| 2 |
| 3 |
| c |
| 3 |
A、[
| ||
| B、[3,+∞) | ||
| C、[-2,3] | ||
| D、(-∞,-2) |
不等式
≤3的解集是( )
| x+1 |
| x |
A、{x|x≥
| ||
B、{x|0<x≤
| ||
C、{x|x>
| ||
D、{x|0≤x<
|
设某种植物由出生算起长到1m的概率为0.8,长到2m的概率为0.4,现有一个1m的这种植物,它能长到2m的概率是( )
| A、0.32 | B、0.4 |
| C、0.5 | D、0.8 |
点P(1,2,z)到点A(1,1,2)、B(2,1,1)的距离相等,则z等于( )
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知复数z=(x2-2x-3)+(x-3)i(x∈R,i为虚数单位)为纯虚数,则x的值为( )
| A、-1或3 | B、0 | C、3 | D、-1 |