题目内容
函数y=2sin（
x+
）的最小正周期是（ ）
| 1 |
| 2 |
| π |
| 3 |
| A、π | B、2π | C、-4π | D、4π |
考点：三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：利用y=Asin（ωx+φ）的周期等于 T=
，计算求得结果．
| 2π |
| ω |
解答：
解：函数y=2sin（
x+
）的最小正周期T=
=4π，
故选：D．
| 1 |
| 2 |
| π |
| 3 |
| 2π | ||
|
故选：D．
点评：本题主要考查三角函数的周期性及其求法，利用了y=Asin（ωx+φ）的周期等于 T=
，属于基础题．
| 2π |
| ω |
练习册系列答案
相关题目
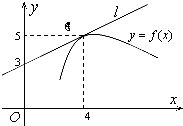
如图，直线l是曲线y=f（x）在x=4处的切线，则f′（4）=（ ）
A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
不等式
≤3的解集是（ ）
| x+1 |
| x |
A、{x|x≥
| ||
B、{x|0＜x≤
| ||
C、{x|x＞
| ||
D、{x|0≤x＜
|
设某种植物由出生算起长到1m的概率为0.8，长到2m的概率为0.4，现有一个1m的这种植物，它能长到2m的概率是（ ）
| A、0.32 | B、0.4 |
| C、0.5 | D、0.8 |
已知向量
=（3，1），
=（x，-1），且
∥
，则实数x的值为（ ）
| a |
| b |
| a |
| b |
| A、-3 | B、3 | C、-1 | D、1 |
点P（1，2，z）到点A（1，1，2）、B（2，1，1）的距离相等，则z等于（ ）
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
在对吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（ ）
| A、若由随机变量求出有95%的把握说吸烟与患肺病有关，那么有5%的可能性使得推断错误 |
| B、若由随机变量求出有95%的把握说吸烟与患肺病有关，那么说明吸烟与患肺病相关程度为95% |
| C、若由随机变量求出有99%的把握说吸烟与患肺病有关，则若某人吸烟，那么他有99%的可能患有肺病 |
| D、若由随机变量求出有99%的把握说吸烟与患肺病有关，则在100个吸烟者中必有99个人患有肺病 |
已知tanα=2，则
=（ ）
| 3sinα+2cosα |
| 3sinα-2cosα |
| A、2 | B、1 | C、4 | D、-4 |