题目内容
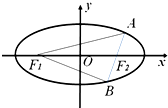已知F1，F2为椭圆的两个焦点，|F1F2|=6，如图△AF1B的顶点A、B在椭圆上，F2在边AB上，其周长为20，则椭圆的离心率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由椭圆的定义，求出a，再求出c，即可求出椭圆的离心率．
解答：
解：由椭圆的定义，4a=20，∴a=5，
又|F1F2|=6，∴2c=6，∴c=3，
∴e=
=
．
故选：B．
又|F1F2|=6，∴2c=6，∴c=3，
∴e=
| c |
| a |
| 3 |
| 5 |
故选：B．
点评：本题考查椭圆的简单几何性质、考查椭圆的定义．属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
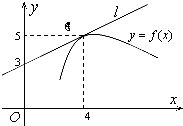
如图，直线l是曲线y=f（x）在x=4处的切线，则f′（4）=（ ）
A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
点P（1，2，z）到点A（1，1，2）、B（2，1，1）的距离相等，则z等于（ ）
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
在对吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（ ）
| A、若由随机变量求出有95%的把握说吸烟与患肺病有关，那么有5%的可能性使得推断错误 |
| B、若由随机变量求出有95%的把握说吸烟与患肺病有关，那么说明吸烟与患肺病相关程度为95% |
| C、若由随机变量求出有99%的把握说吸烟与患肺病有关，则若某人吸烟，那么他有99%的可能患有肺病 |
| D、若由随机变量求出有99%的把握说吸烟与患肺病有关，则在100个吸烟者中必有99个人患有肺病 |
如图程序执行后输出的结果是（ ）
| A、1 | B、2 | C、3 | D、4 |
函数f（x）=ex+x2-2的零点的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
已知复数z=（x2-2x-3）+（x-3）i（x∈R，i为虚数单位）为纯虚数，则x的值为（ ）
| A、-1或3 | B、0 | C、3 | D、-1 |
已知tanα=2，则
=（ ）
| 3sinα+2cosα |
| 3sinα-2cosα |
| A、2 | B、1 | C、4 | D、-4 |
如图四边形ABEF是等腰梯形，AB∥EF，AF=BE=2，EF=4