题目内容

函数y=x3+log2x+2ex的导数为
 
．
考点：导数的运算
专题：导数的概念及应用
分析：根据函数的导数公式，之间进行求解即可．
解答： 解：∵y=x3+log2x+2ex，
∴y′=3x2+
1
xln2
+2ex，
故答案为：y′=3x2+
1
xln2
+2ex．
点评：本题主要考查导数的计算，要求熟练掌握常见函数的导数公式，比较基础．
练习册系列答案
相关题目
若数列：12+22+32+42+…+n2=
n(n+1)(2n+1)
6
，则数列：1，2，2，3，3，3，4，4，4，4，…的前100项的和是
 
．
已知双曲线
x2
a2
-
y2
b2
=λ（a＞0，b＞0，λ≠0）的渐近线经过点（2，1），则双曲线的离心率e=
 
．
将正整数排成如图所示，则300应出现在数表中第
 
行第
 
个数．
已知平面直角坐标系xOy，以O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的参数方程为
x=2cosφ
y=2+2sinφ
，（φ为参数）．点A，B是曲线C上两点，点A，B的极坐标分别为（ρ1，
π
3
），（ρ2，
5π
6
）．
（1）写出曲线C的普通方程和极坐标方程；
（2）求|AB|的值．
已知线段AB为圆O的弦，且AB=4，则
AO
•
AB
=
 
．
下列结论中：
①函数y=x（1-2x）（x＞0）有最大值
1
8

②函数y=2-3x-
4
x
（x＜0）有最大值2-4
3

③若a＞0，则(1+a)(1+
1
a
)≥4
正确的序号是
 
．
如图，直线l是曲线y=f（x）在x=4处的切线，则f′（4）=（　　）
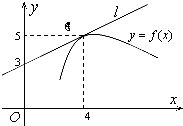
A、
1
2
B、3
C、4
D、5
点P（1，2，z）到点A（1，1，2）、B（2，1，1）的距离相等，则z等于（　　）
A、
1
2
B、
3
2
C、1
D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网