Question

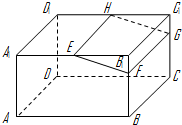如图，在长方体ABCD-A₁B₁C₁D₁中，E，H分别是棱A₁B₁，D₁C₁上的点（点E与B₁不重合），且EH∥A₁D₁，过EH的平面与棱BB₁，CC₁相交，交点分别为F，G．设AB=2AA₁=2a，EF=a，B₁E=B₁F．在长方体ABCD-A₁B₁C₁D₁内随机选取一点，则该点取自于几何体A₁ABFE-D₁DCGH内的概率为（　　）

• A、

  11

  16

• B、

  3

  4

• C、

  13

  16

• D、

  7

  8

Answer 1

考点：几何概型

专题：概率与统计

分析：求出对应区域的体积，利用几何概型的概率公式即可得到结论．

解答： 解：∵EH∥A₁D₁，过EH的平面与棱BB₁，CC₁相交，交点分别为F，G．
∴FG∥EH，
即几何体B₁FE-C₁GH是三棱柱，
∵AB=2AA₁=2a，EF=a，B₁E=B₁F．
∴△B₁FE为等腰直角三角形，
且B₁E=B₁F=

2

2

a，
则三棱柱B₁FE-C₁GH的体积V=

1

2

×(

2

2

a)2×B1C1=

B1C1

4

•a2，
长方体的体积V=2a•a•B₁C₁=2a²•B₁C₁，
则几何体A₁ABFE-D₁DCGH的体积V₁=2a²•B₁C₁-

1

4

a²•B₁C₁=

7

4

a²•B₁C₁，
则根据几何概型的概率公式可得在长方体ABCD-A₁B₁C₁D₁内随机选取一点，则该点取自于几何体A₁ABFE-D₁DCGH内的概率
P=

V1

V长方体

=

7 4 a2•B1C1

2a2B1C1

=

7

8

，
故选：D

点评：本题主要考查几何概型的概率计算以及空间几何体的体积计算，根据条件求出对应的几何体的体积是解决本题的关键．