题目内容
在函数y=sin|x|、y=|sinx|、y=tan（2x+
）、y=cos（-2x+
）中，最小正周期为π的函数的个数为（ ）
| 2π |
| 3 |
| 2π |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
考点：三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：根据三角函数的周期性，先求出各个函数的周期，从而得出结论．
解答：
解：由于函数y=sin|x|没有周期性，故不满足条件．
由于y=|sinx|的周期为
×2π=π，故满足条件．
由于y=tan（2x+
）的周期为
，故不满足条件．
由于函数y=cos（-2x+
）=cos（2x-
），它的最小正周期为
=π，故满足条件，
故选：B．
由于y=|sinx|的周期为
| 1 |
| 2 |
由于y=tan（2x+
| 2π |
| 3 |
| π |
| 2 |
由于函数y=cos（-2x+
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 2 |
故选：B．
点评：本题主要考查三角函数的周期性和求法，属于基础题．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
已知关于
的方程有3（
+
）=
，则
=（ ）
| x |
| a |
| x |
| x |
| x |
A、
| ||||
B、-
| ||||
C、
| ||||
| D、无解 |
已知a=20.3，b=log0.50.24，c=0.32，则a，b，c的大小关系正确的是（ ）
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＜a＜b |
| D、b＜c＜a |
函数y=
的定义域为（ ）
| ||
| tanx |
| A、（0，3] | ||||
| B、（0，π） | ||||
C、（0，
| ||||
D、[0，
|
已知f（x）=
，则f（-8）等于（ ）
|
| A、-1 | B、0 | C、1 | D、2 |
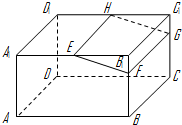如图，在长方体ABCD-A1B1C1D1中，E，H分别是棱A1B1，D1C1上的点（点E与B1不重合），且EH∥A1D1，过EH的平面与棱BB1，CC1相交，交点分别为F，G．设AB=2AA1=2a，EF=a，B1E=B1F．在长方体ABCD-A1B1C1D1内随机选取一点，则该点取自于几何体A1ABFE-D1DCGH内的概率为（ ）
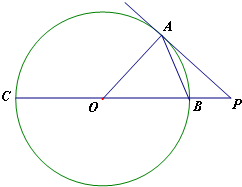如图，点A在直径为15的⊙O上，PBC是过点O的割线，且PA=10，PB=5．
如图，已知AB⊥平面ACD，DE⊥平面ACD，AB=2，AC=AD=DE=4，F为CD的中点，