题目内容
函数y=
的定义域为（ ）
| sinx |
| A、[0，π] |
| B、x为第Ⅰ、Ⅱ象限的角 |
| C、{x|2kπ≤x≤（2k+1）π，k∈z} |
| D、（0，π） |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件，即可求函数的定义域．
解答：
解：要使函数有意义，则sinx≥0，
即2kπ≤x≤（2k+1）π，k∈z．
故函数的定义域为{x|2kπ≤x≤（2k+1）π，k∈z}，
故选：C．
即2kπ≤x≤（2k+1）π，k∈z．
故函数的定义域为{x|2kπ≤x≤（2k+1）π，k∈z}，
故选：C．
点评：本题主要考查函数定义域的求法，根据函数成立的条件以及三角函数的图象和性质是解决此类问题的关键．
练习册系列答案
相关题目
已知0＜x＜4.5，当x2（9-2x）取得最大值时，x取何值（ ）
| A、1 | B、2 | C、3 | D、27 |
给出命题：若cosα=
，则α=
．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是（ ）
| 1 |
| 2 |
| π |
| 3 |
| A、3 | B、2 | C、1 | D、0 |
在平面直角坐标系xOy中，已知平面向量
=（a，0），
=（0，b），其中a，b为[-2，2]上的两个随机实数，定义平面上的点集Ω，Ω1，Φ分别为Ω={P|
=
+
}，Ω1={Q|
|=|
|=
且|QP|＜1，P∈Ω}，Φ：Ω1∪{R|
＜|
|＜2}．若在Ω对应的平面区域内随机取一个点W，则点W落在Φ对应的平面区域内的概率为（ ）
| ON1 |
| ON2 |
| OP |
| ON1 |
| ON2 |
| QN1 |
| QN2 |
| 2 |
| 3 |
| OR |
A、
| ||
B、1-
| ||
C、
| ||
D、
|
函数y=
的定义域为（ ）
| ||
| tanx |
| A、（0，3] | ||||
| B、（0，π） | ||||
C、（0，
| ||||
D、[0，
|
若x=
，则sin4x-cos4x的值为（ ）
| π |
| 12 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
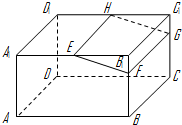如图，在长方体ABCD-A1B1C1D1中，E，H分别是棱A1B1，D1C1上的点（点E与B1不重合），且EH∥A1D1，过EH的平面与棱BB1，CC1相交，交点分别为F，G．设AB=2AA1=2a，EF=a，B1E=B1F．在长方体ABCD-A1B1C1D1内随机选取一点，则该点取自于几何体A1ABFE-D1DCGH内的概率为（ ）
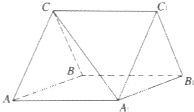如图，三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°．