题目内容
已知函数f(x)=x-alnx-1.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)设a=2,对于任意的x∈[1,2],函数g(x)=x3+x2[f′(x)+
]在区间(2,3)上不是单调函数,求实数m的取值范围.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)设a=2,对于任意的x∈[1,2],函数g(x)=x3+x2[f′(x)+
| m |
| 2 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)中通过求导讨论a的取值范围确定单调区间,(Ⅱ)中先求出g(x)的表达式,再通过求导得出不等式组,从而确定m的取值范围.
解答:
解:(Ⅰ)由题意得:f(x)的定义域为:{x|x>0},
又∵f′(x)=1-
,
①当a≤0时,f′(x)>0,
∴f(x)在(0,+∞)上单调递增;
②当a>0时,
令f(x)>0,解得:x>a,f(x)在(a,+∞)上单调递增,
令f(x)<0,解得:0<x<a,f(x)在(0,a)上单调递减;
综上所述:
当a≤0时,f(x)在(0,+∞)上单调递增;
当a>0时,f(x)在(a,+∞)上单调递增,在(0,a)上单调递减.
(Ⅱ)当a=2时,f(x)=x-2lnx-1,
∴f′(x)=1-
,
∴g(x)=x3+(1+
)x2-2x,
∴g′(x)=3x2+(2-m)x-2,
又g′(0)=-2,g(x)在(2,3)上不是单调函数,
∴
即:
,
解得:-
<m<-7.
∴实数m的范围是:(-
,-7).
又∵f′(x)=1-
| a |
| x |
①当a≤0时,f′(x)>0,
∴f(x)在(0,+∞)上单调递增;
②当a>0时,
令f(x)>0,解得:x>a,f(x)在(a,+∞)上单调递增,
令f(x)<0,解得:0<x<a,f(x)在(0,a)上单调递减;
综上所述:
当a≤0时,f(x)在(0,+∞)上单调递增;
当a>0时,f(x)在(a,+∞)上单调递增,在(0,a)上单调递减.
(Ⅱ)当a=2时,f(x)=x-2lnx-1,
∴f′(x)=1-
| 2 |
| x |
∴g(x)=x3+(1+
| m |
| 2 |
∴g′(x)=3x2+(2-m)x-2,
又g′(0)=-2,g(x)在(2,3)上不是单调函数,
∴
|
|
解得:-
| 31 |
| 3 |
∴实数m的范围是:(-
| 31 |
| 3 |
点评:本题考察了求导函数,讨论函数的单调区间,导函数的应用,是一道综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设全集 U={1,2,3,4,5,6,7},M={2,3,4,6},N={1,4,5},则(∁UM)∩N 等于( )
| A、{1,2,4,5,7} |
| B、{1,4,5} |
| C、{1,5} |
| D、{1,4} |
函数y=
的定义域为( )
| ||
| tanx |
| A、(0,3] | ||||
| B、(0,π) | ||||
C、(0,
| ||||
D、[0,
|
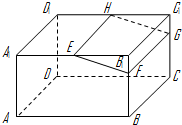 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为( )
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为( )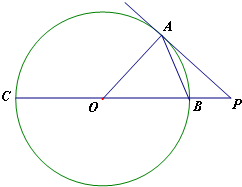 如图,点A在直径为15的⊙O上,PBC是过点O的割线,且PA=10,PB=5.
如图,点A在直径为15的⊙O上,PBC是过点O的割线,且PA=10,PB=5.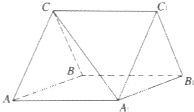 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°. 如图,已知AB⊥平面ACD,DE⊥平面ACD,AB=2,AC=AD=DE=4,F为CD的中点,
如图,已知AB⊥平面ACD,DE⊥平面ACD,AB=2,AC=AD=DE=4,F为CD的中点,