题目内容
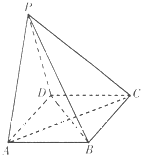 如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=
如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=| 2 |
(Ⅰ)求证:PC⊥BD;
(Ⅱ)若四棱锥P-ABCD的体积为
4
| ||
| 3 |
考点:与二面角有关的立体几何综合题,棱柱、棱锥、棱台的体积
专题:空间角
分析:(Ⅰ)取O为AD的中点,连接CO,PO,由已知条件推导出Rt△CDO∽Rt△DAB,从而得到BD⊥OC,由此能够证明PC⊥BD.
(Ⅱ)由等体积法坟出PO=2,建立空间直角坐标系,利用向量法能求出二面角A-PC-D的余弦值.
(Ⅱ)由等体积法坟出PO=2,建立空间直角坐标系,利用向量法能求出二面角A-PC-D的余弦值.
解答:
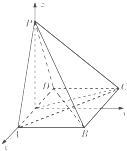 (Ⅰ)证明:取O为AD的中点,连接CO,PO,如下图.
(Ⅰ)证明:取O为AD的中点,连接CO,PO,如下图.
则在矩形ABCD中,∵
=
=
,∴Rt△CDO∽Rt△DAB,
∴∠OCD=∠BDA,∴∠OCD+∠CDB=90°,
∴BD⊥OC,…(3分)
∵PA=PD,O为AD中点,∴PO⊥AD,又平面PAD⊥平面ABCD.
∴PO⊥平面ABCD,∴PO⊥BD.
又OC?平面POC,PO?平面POC,∴BD⊥平面POC,
又PC?平面POC,∴PC⊥BD.…(6分)
(Ⅱ)解:由VP-ABCD=
S矩形ABCD•PO=
×2×
•PO=
,解得PO=2,…(7分)
建立如图所示空间直角坐标系,则有
A(1,0,0),P(0,0,2),C(-1,
,0),D(-1,0,0),
∴
=(-1,0,2),
=(-2,
,0),
=(1,0,2),
=(0,
,0).…(8分)
设平面PAC的一个法向量为
n1=(x1,y1,z1),
则有
,即
,令z1=1,得
=(2,2
,1),
同理,设平面PAD的一个法向量为
=(x2,y2,z2),
则有
,即
,令x2=2,得
=(2,0,-1),
cos?n1,n2>=
=
=
,…(10分)
由图可知二面角A-PC-D为锐二面角,
故二面角A-PC-D的余弦值为
.…(12分)
 (Ⅰ)证明:取O为AD的中点,连接CO,PO,如下图.
(Ⅰ)证明:取O为AD的中点,连接CO,PO,如下图.则在矩形ABCD中,∵
| CD |
| AD |
| DO |
| AB |
| ||
| 2 |
∴∠OCD=∠BDA,∴∠OCD+∠CDB=90°,
∴BD⊥OC,…(3分)
∵PA=PD,O为AD中点,∴PO⊥AD,又平面PAD⊥平面ABCD.
∴PO⊥平面ABCD,∴PO⊥BD.
又OC?平面POC,PO?平面POC,∴BD⊥平面POC,
又PC?平面POC,∴PC⊥BD.…(6分)
(Ⅱ)解:由VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
4
| ||
| 3 |
建立如图所示空间直角坐标系,则有
A(1,0,0),P(0,0,2),C(-1,
| 2 |
∴
| AP |
| AC |
| 2 |
| DP |
| DC |
| 2 |
设平面PAC的一个法向量为
| n1 |
则有
|
|
| n1 |
| 2 |
同理,设平面PAD的一个法向量为
| n2 |
则有
|
|
| n2 |
cos?n1,n2>=
| n1•n2 |
| |n1|•|n2| |
| 4-1 | ||||
|
3
| ||
| 65 |
由图可知二面角A-PC-D为锐二面角,
故二面角A-PC-D的余弦值为
3
| ||
| 65 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
如果α在第二象限,则
必定在( )
| α |
| 2 |
| A、第一或第二象限 |
| B、第一或第三象限 |
| C、第三或第四象限 |
| D、第二或第四象限 |
在平面直角坐标系xOy中,已知平面向量
=(a,0),
=(0,b),其中a,b为[-2,2]上的两个随机实数,定义平面上的点集Ω,Ω1,Φ分别为Ω={P|
=
+
},Ω1={Q|
|=|
|=
且|QP|<1,P∈Ω},Φ:Ω1∪{R|
<|
|<2}.若在Ω对应的平面区域内随机取一个点W,则点W落在Φ对应的平面区域内的概率为( )
| ON1 |
| ON2 |
| OP |
| ON1 |
| ON2 |
| QN1 |
| QN2 |
| 2 |
| 3 |
| OR |
A、
| ||
B、1-
| ||
C、
| ||
D、
|
若x=
,则sin4x-cos4x的值为( )
| π |
| 12 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
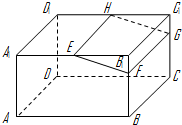 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为( )
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为( )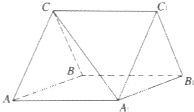 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.