题目内容
若函数f（x）=
的定义域是（ ）
| (x+1)0 | ||
|
| A、（-∞，-1） |
| B、（-1，0） |
| C、（-1，1） |
| D、（-∞，-1）∪（-1，0） |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件，即可求函数的定义域．
解答：
解：要使函数有意义，则
，
即
即x＜0且x≠-1，
故函数的定义域为（-∞，-1）∪（-1，0），
故选：D．
|
即
|
即x＜0且x≠-1，
故函数的定义域为（-∞，-1）∪（-1，0），
故选：D．
点评：本题主要考查函数定义域的求法，根据函数成立的条件是解决此类问题的关键．
练习册系列答案
相关题目
已知三次函数f（x）=ax3+bx2+cx+d的图象如图所示，则| f′(-3) |
| f′(1) |
| A、-1 | B、2 | C、-5 | D、-3 |
设全集 U={1，2，3，4，5，6，7}，M={2，3，4，6}，N={1，4，5}，则（∁UM）∩N 等于（ ）
| A、{1，2，4，5，7} |
| B、{1，4，5} |
| C、{1，5} |
| D、{1，4} |
给出命题：若cosα=
，则α=
．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是（ ）
| 1 |
| 2 |
| π |
| 3 |
| A、3 | B、2 | C、1 | D、0 |
已知a=20.3，b=log0.50.24，c=0.32，则a，b，c的大小关系正确的是（ ）
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＜a＜b |
| D、b＜c＜a |
在平面直角坐标系xOy中，已知平面向量
=（a，0），
=（0，b），其中a，b为[-2，2]上的两个随机实数，定义平面上的点集Ω，Ω1，Φ分别为Ω={P|
=
+
}，Ω1={Q|
|=|
|=
且|QP|＜1，P∈Ω}，Φ：Ω1∪{R|
＜|
|＜2}．若在Ω对应的平面区域内随机取一个点W，则点W落在Φ对应的平面区域内的概率为（ ）
| ON1 |
| ON2 |
| OP |
| ON1 |
| ON2 |
| QN1 |
| QN2 |
| 2 |
| 3 |
| OR |
A、
| ||
B、1-
| ||
C、
| ||
D、
|
函数y=
的定义域为（ ）
| ||
| tanx |
| A、（0，3] | ||||
| B、（0，π） | ||||
C、（0，
| ||||
D、[0，
|
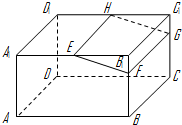如图，在长方体ABCD-A1B1C1D1中，E，H分别是棱A1B1，D1C1上的点（点E与B1不重合），且EH∥A1D1，过EH的平面与棱BB1，CC1相交，交点分别为F，G．设AB=2AA1=2a，EF=a，B1E=B1F．在长方体ABCD-A1B1C1D1内随机选取一点，则该点取自于几何体A1ABFE-D1DCGH内的概率为（ ）