题目内容
过点P(-10,0)引直线l与曲线y=-
相交于A,B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于 .
| 50-x2 |
考点:直线与圆的位置关系
专题:直线与圆
分析:由题意可知曲线为单位圆在x轴上方部分(含与x轴的交点),由此可得到过C点的直线与曲线相交时k的范围,设出直线方程,由点到直线的距离公式求出原点到直线的距离,由勾股定理求出直线被圆所截半弦长,写出面积后利用配方法转化为求二次函数的最值.
解答:
解:曲线y=-
即 x2+y2=50 (y≤0),表示以原点为圆心,半径等于5
的下半圆.
设直线l的斜率为k,则直线l的方程为y-0=k(x+10),即y=kx+10k.
由于弦心距d=
=
,∴弦长AB=2
=2
,
∴S△OAB=
•d•AB=
•
=
=50
=
=
.
令
=t∈(0,1],则S△OAB=
,故当t=
时,S△OAB取得最大值为
,
此时,由t=
,k=
(不合题意,舍去),或k=-
,
故答案为:-
.
| 50-x2 |
| 2 |
设直线l的斜率为k,则直线l的方程为y-0=k(x+10),即y=kx+10k.
由于弦心距d=
| |0-0+10k| | ||
|
| |10k| | ||
|
| r2-d2 |
|
∴S△OAB=
| 1 |
| 2 |
| |10k| | ||
|
|
50
| ||
| k2+1 |
|
=
|
-2+
|
令
| 1 |
| k2+1 |
| -4t2+6t-2 |
| 3 |
| 4 |
| 1 |
| 2 |
此时,由t=
| 3 |
| 4 |
| ||
| 3 |
| ||
| 3 |
故答案为:-
| ||
| 3 |
点评:本题考查了直线的斜率,考查了直线与圆的关系,考查了学生的运算能力,考查了配方法及二次函数求最值,解答此题的关键在于把面积表达式转化为二次函数求最值,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
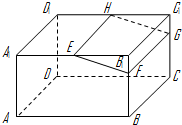 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为( )
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
将函数y=sin2x的图象向右平移
个单位后,所得图象的一条对称轴方程是( )
| π |
| 8 |
A、x=
| ||
B、x=-
| ||
C、x=
| ||
D、x=-
|