题目内容
讨论函数f(x)=
cos(2x-2a)+cos2a-2cos(x-a)•cosx•cosa的周期、最值、奇偶性及单调区间.
| 1 |
| 2 |
考点:三角函数的周期性及其求法,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:利用三角函数的恒等变换化简函数的及诶小时为f(x)=-
cos2x,由此求得函数的周期、最大值、最小值、奇偶性,再利用函数的单调性和y=cos2x的单调性相反,求得此函数的单调区间.
| 1 |
| 2 |
解答:
解:函数f(x)=
cos(2x-2a)+cos2a-2cos(x-a)•cosx•cosa
=
[2cos2(x-a)-1]+
-2cos(x-a)•
[cos(x-a)+cos(x+a)]
=cos2(x-a)+
cos2a-cos2(x-a)-cos(x-a)•cos(x+a)
=
cos2a-
[cos2a+cos2x]=-
cos2x,
故函数的周期为
=π,最大值为
,最小值为-
.
根据余弦函数的奇偶性可得此函数为偶函数.
由于函数的单调性和y=cos2x的单调性相反,
令2kπ-π≤2x≤2kπ,k∈z,求得 kπ-
≤x≤kπ,可得函数减区间为[kπ-
,kπ],k∈z.
令2kπ≤2x≤2kπ+π,k∈z,求得 kπ≤x≤kπ+
,可得函数增区间为[kπ,kπ+
],k∈z.
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1+cos2a |
| 2 |
| 1 |
| 2 |
=cos2(x-a)+
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故函数的周期为
| 2π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
根据余弦函数的奇偶性可得此函数为偶函数.
由于函数的单调性和y=cos2x的单调性相反,
令2kπ-π≤2x≤2kπ,k∈z,求得 kπ-
| π |
| 2 |
| π |
| 2 |
令2kπ≤2x≤2kπ+π,k∈z,求得 kπ≤x≤kπ+
| π |
| 2 |
| π |
| 2 |
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性、单调性、最值、奇偶性,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
给出命题:若cosα=
,则α=
.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )
| 1 |
| 2 |
| π |
| 3 |
| A、3 | B、2 | C、1 | D、0 |
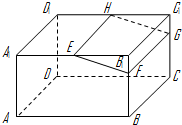 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为( )
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为( )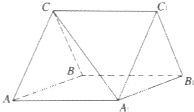 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°. 如图,已知AB⊥平面ACD,DE⊥平面ACD,AB=2,AC=AD=DE=4,F为CD的中点,
如图,已知AB⊥平面ACD,DE⊥平面ACD,AB=2,AC=AD=DE=4,F为CD的中点,