题目内容
2.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≤0}\\{x+y-7≤0}\\{x-1≥0}\\{\;}\end{array}\right.$,则Z=$\frac{y+x}{x}$的取值范围为( )| A. | [$\frac{14}{5}$,7] | B. | [4,7] | C. | [$\frac{14}{5}$,4] | D. | [7,+∞) |
分析 作出不等式组对应的平面区域,利用直线斜率的几何意义进行求解即可.
解答 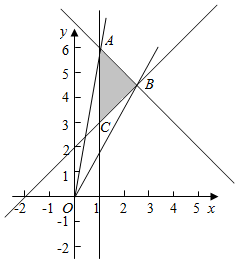 解:作出不等式组对应的平面区域如图,
解:作出不等式组对应的平面区域如图,
Z=$\frac{y+x}{x}$=$\frac{y}{x}$+1
设k=$\frac{y}{x}$,在k的几何意义是区域内的点到原点的斜率,
由图象知OA的斜率最大,OB的斜率最小,
由$\left\{\begin{array}{l}{x=1}\\{x+y-7=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$,得A(1,6),此时k=6,
由$\left\{\begin{array}{l}{x-y+2=0}\\{x+y-7=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=\frac{9}{2}}\end{array}\right.$,即B($\frac{5}{2}$,$\frac{9}{2}$),
此时k=$\frac{\frac{9}{2}}{\frac{5}{2}}$=$\frac{9}{5}$,$\frac{9}{5}$≤k≤6,
则$\frac{14}{5}$≤k+1≤7,
即Z=$\frac{y+x}{x}$的取值范围为[$\frac{14}{5}$,7],
故选:A
点评 本题主要考查线性规划的应用,利用目标函数的几何意义结合两点间的斜率公式进行转化求解是解决本题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
13.已知函数y=2sin(ωx+φ)(ω>0,0<φ<π)的图象上相邻两个最高点的距离为π,若将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度后,所得图象关于x=$\frac{π}{4}$轴对称,则f(x)的解析式为( )
| A. | f(x)=2sin(x+$\frac{π}{6}$) | B. | f(x)=2sin(2x+$\frac{2π}{3}$) | C. | f(x)=2sin(x+$\frac{π}{3}$) | D. | f(x)=2sin(2x+$\frac{5π}{6}$) |
17.圆x2+y2-4x=0的圆心到双曲线$\frac{{x}^{2}}{3}$-y2=1的渐近线的距离为( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
14.设集合A={x|x2+x-6<0},B={x|x<0},则A∩∁RB=( )
| A. | {x|0≤x<2} | B. | {x|-3<x<2} | C. | {x|-6<x<0} | D. | {x|x≥0} |
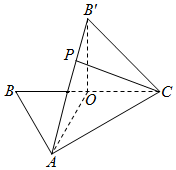 如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2,将△BAO沿AO折起,使B点到达B′点.
如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2,将△BAO沿AO折起,使B点到达B′点.