题目内容
17.圆x2+y2-4x=0的圆心到双曲线$\frac{{x}^{2}}{3}$-y2=1的渐近线的距离为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 求得圆的圆心和半径,双曲线的渐近线方程,运用点到直线的距离公式,计算即可得到所求值.
解答 解:圆x2+y2-4x=0的圆心为(2,0),半径为2,
双曲线$\frac{{x}^{2}}{3}$-y2=1的渐近线方程为y=±$\frac{\sqrt{3}}{3}$x,
可得圆心到双曲线$\frac{{x}^{2}}{3}$-y2=1的渐近线的距离为:
d=$\frac{\frac{2\sqrt{3}}{3}}{\sqrt{1+\frac{1}{3}}}$=1.
故选:A.
点评 本题考查圆心到渐近线的距离,注意运用点到直线的距离公式,考查运算能力,属于基础题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
5.已知函数f(x)=x|x-a|
(1)判断f(x)的奇偶性,并证明;
(2)求实数a的取值范围,使函数g(x)=f(x)+2x+1在R上恒为增函数;
(3)求函数f(x)在[-1,1]的最小值g(a).
(1)判断f(x)的奇偶性,并证明;
(2)求实数a的取值范围,使函数g(x)=f(x)+2x+1在R上恒为增函数;
(3)求函数f(x)在[-1,1]的最小值g(a).
12.设a,b∈R,那么“ln$\frac{a}{b}$>0”是“a>b>0”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
2.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≤0}\\{x+y-7≤0}\\{x-1≥0}\\{\;}\end{array}\right.$,则Z=$\frac{y+x}{x}$的取值范围为( )
| A. | [$\frac{14}{5}$,7] | B. | [4,7] | C. | [$\frac{14}{5}$,4] | D. | [7,+∞) |
9.等比数列{an}中,a1•a7=4,则a22+a62的最小值为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
6.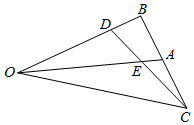 如图:已知,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则△OEC与△OBC的面积的比值是( )
如图:已知,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则△OEC与△OBC的面积的比值是( )
 如图:已知,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则△OEC与△OBC的面积的比值是( )
如图:已知,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则△OEC与△OBC的面积的比值是( )| A. | $\frac{4}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{8}$ |
7.已知集合A={-1,0,1},B={x|y=x2,x∈R},则A∩B=( )
| A. | {0,1} | B. | {-1,0,1} | C. | {1} | D. | ∅ |