题目内容
13.已知函数y=2sin(ωx+φ)(ω>0,0<φ<π)的图象上相邻两个最高点的距离为π,若将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度后,所得图象关于x=$\frac{π}{4}$轴对称,则f(x)的解析式为( )| A. | f(x)=2sin(x+$\frac{π}{6}$) | B. | f(x)=2sin(2x+$\frac{2π}{3}$) | C. | f(x)=2sin(x+$\frac{π}{3}$) | D. | f(x)=2sin(2x+$\frac{5π}{6}$) |
分析 由周期求出ω,根据y=Asin(ωx+φ)的图象变换规律、正弦函数的对称性,求出φ的值,可得函数的解析式.
解答 解:由题意知:$\frac{2π}{ω}$=π,得ω=2,向左平移$\frac{π}{6}$个单位长度后得f(x)=2sin(2x+$\frac{π}{3}$+φ),
因为,所得图象关于x=$\frac{π}{4}$轴对称,
所以,$\frac{π}{2}$+$\frac{π}{3}$+φ=kπ+$\frac{π}{2}$,k∈Z,
所以,φ=kπ-$\frac{π}{3}$,k∈Z,
因为,0<φ<π,
所以,φ=$\frac{2π}{3}$.
可得f(x)的解析式为f(x)=2sin(2x+$\frac{2π}{3}$).
故选:B.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,y=Asin(ωx+φ)的图象变换规律,由周期求出ω,根据正弦函数的对称性求出φ的值是解题的关键,属于基础题.

练习册系列答案
相关题目
5.已知函数f(x)=x|x-a|
(1)判断f(x)的奇偶性,并证明;
(2)求实数a的取值范围,使函数g(x)=f(x)+2x+1在R上恒为增函数;
(3)求函数f(x)在[-1,1]的最小值g(a).
(1)判断f(x)的奇偶性,并证明;
(2)求实数a的取值范围,使函数g(x)=f(x)+2x+1在R上恒为增函数;
(3)求函数f(x)在[-1,1]的最小值g(a).
2.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≤0}\\{x+y-7≤0}\\{x-1≥0}\\{\;}\end{array}\right.$,则Z=$\frac{y+x}{x}$的取值范围为( )
| A. | [$\frac{14}{5}$,7] | B. | [4,7] | C. | [$\frac{14}{5}$,4] | D. | [7,+∞) |
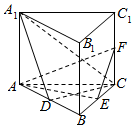 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.