题目内容
12.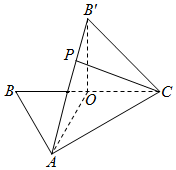 如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2,将△BAO沿AO折起,使B点到达B′点.
如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2,将△BAO沿AO折起,使B点到达B′点.(Ⅰ)求证:AO⊥平面B′OC;
(Ⅱ)当三棱锥B′-AOC的体积最大时,试问在线段B′A上是否存在一点P,使CP与平面B′OA所成的角的正弦值为$\frac{{\sqrt{6}}}{3}$?若存在,求出点P的位置;若不存在,请说明理由.
分析 (I)翻折前,由三线合一可知OA⊥BC,故翻折后OA⊥OB′,OA⊥OC,于是AO⊥平面B′OC;
(II)当OB⊥平面AOC时,三棱锥B′-AOC的体积最大,此时可证OC⊥平面AOB′,故∠CPO为CP与平面B′OA所成的角,利用直角三角形知识解出OP,与O到线段AB′的距离的范围比较即可得出结论.
解答  (Ⅰ)证明:∵AB=AC,O是BC的中点,
(Ⅰ)证明:∵AB=AC,O是BC的中点,
∴AO⊥BO,AO⊥CO,即AO⊥B′O,
又CO∩B′O=O,B′O?平面B′OC,OC?平面B′OC,
∴AO⊥平面B′OC.
(Ⅱ)解:不存在.证明如下:
当面B′OA⊥面AOC时,三棱锥B′-AOC的体积最大.
∵面B′OA⊥面AOC,面B′OA∩面AOC=AO,OC⊥AO,OC?平面AOC,
∴CO⊥面B′OA,
∴∠CPO即为直线CP与平面B′OA所成的角,
在直角三角形CPO中,$CO=1,∠COP=\frac{π}{2},sin∠CPO=\frac{{\sqrt{6}}}{3}$,
∴$CP=\frac{3}{{\sqrt{6}}}$,∴OP=$\sqrt{P{C}^{2}-O{C}^{2}}$=$\frac{\sqrt{2}}{2}$.
在△AOB′中,∠AOB′=90°,AB′=$\sqrt{O{A}^{2}+OB{′}^{2}}=\sqrt{5}$,设△AOB′的边AB′上的高为h,
则h=$\frac{OA•OB}{AB′}$=$\frac{2\sqrt{5}}{5}$.
因为OP<h,所以满足条件的点P不存在.
点评 本题考查了线面垂直的判定,线面角的做法与计算,属于中档题.

练习册系列答案
相关题目
15.给出下列4个命题,其中正确的个数是( )
①若“命题p∧q为真”,则“命题p∨q为真”;
②命题“?x>0,x-lnx>0”的否定是“?x>0,x-lnx≤0”;
②“tanx>0”是“sin2x>0”的充要条件;
④计算:9192除以100的余数是1.
①若“命题p∧q为真”,则“命题p∨q为真”;
②命题“?x>0,x-lnx>0”的否定是“?x>0,x-lnx≤0”;
②“tanx>0”是“sin2x>0”的充要条件;
④计算:9192除以100的余数是1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≤0}\\{x+y-7≤0}\\{x-1≥0}\\{\;}\end{array}\right.$,则Z=$\frac{y+x}{x}$的取值范围为( )
| A. | [$\frac{14}{5}$,7] | B. | [4,7] | C. | [$\frac{14}{5}$,4] | D. | [7,+∞) |
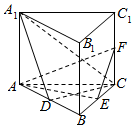 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.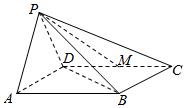 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.